Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
Para ello, sólo hay que ver que $K$ y $L$ tienen la misma potencia respecto de ambas circunferencias, lo que equivale a decir que $LB\cdot LF=LE\cdot LA$ y $KD\cdot KG=KC\cdot KH$. Sin embargo, la primera igualdad se deduce directamente de que los triángulos $LFA$ y $LEB$ son semejantes, mientras que la segunda viene de que $KGC$ y $KDH$ son semejantes. En ambos casos se trata de triángulos rectángulos con un ángulo (no recto) común.
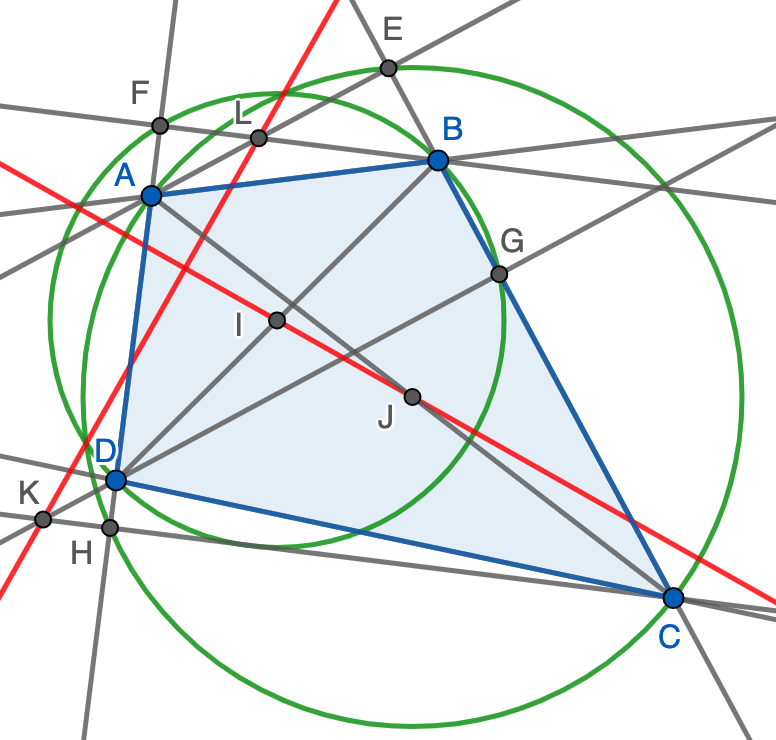
Nota. La demostración vale tanto si el cuadrilátero es cóncavo o convexo, o incluso si no hay cuadrilátero sino solo cuatro puntos dados en el plano. La única salvedad es que $ABCD$ sea un paralelogramo, en cuyo caso $I=J$ (y, por tanto, la recta $IJ$ no está definida) y $K$ y $L$ no existen ya que las rectas cuya intersección los define son paralelas.
Informar de error en enunciado Informar de procedencia del problema