Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
Con todo esto ya podemos calcular el área de $AECF$ puesto que esta consta de los dos triángulos equiláteros $ADM$ y $DMC$ (en azul en la figura). Ambos tienen lado $\ell=5$, luego su área es $\frac{\ell^2\sqrt{3}}{4}=\frac{25\sqrt{3}}{4}$ (esto se comprueba fácilmente usando el teorema de Pitágoras). También tenemos que contar los dos triángulos congruentes $DEC$ y $CMF$ (en amarillo en la figura), que tienen la misma altura que los equiláteros pero un tercio de su base, luego cada uno aporta un tercio del área ya calculada $\frac{25\sqrt{3}}{4}$. En resumen, tenemos que
\begin{align*}
\mathrm{Area}(AECF)&=\mathrm{Area}(ADM)+\mathrm{Area}(DMC)+\mathrm{Area}(DEC)+\mathrm{Area}(CMF)\\
&=\frac{25\sqrt{3}}{4}+\frac{25\sqrt{3}}{4}+\frac{1}{3}\cdot\frac{25\sqrt{3}}{4}+\frac{1}{3}\cdot\frac{25\sqrt{3}}{4}=\frac{50\sqrt{3}}{3}.
\end{align*}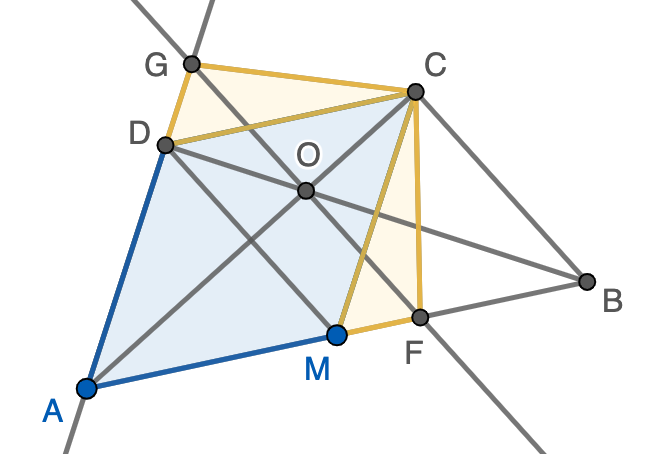
Informar de error en enunciado Informar de procedencia del problema