Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 582
En un triángulo $ABC$ con lado mayor $BC$, las bisectrices se cortan en $I$. Las rectas $AI$, $BI$ y $CI$ cortan a $BC$, $CA$, $AB$ en los puntos $D$, $E$ y $F$, respectivamente. Se consideran puntos $G$ y $H$ en los segmentos $BD$ y $CD$, respectivamente, tales que $\angle GID = \angle ABC$ y $\angle HID =\angle ACB$. Probar que $\angle BHE = \angle CGF$.
pistasolución 1info
Pista. ¡Caza ángulos y triángulos semejantes!
Solución. Sean $\angle CAB=2\alpha$, $\angle ABC=2\beta$ y $\angle BCA=2\gamma$. El triángulo $ABD$ tiene un ángulo igual a $2\beta$ y otro igual a $\alpha$, luego el tercero es $\angle GDI=180-2\beta-\alpha=\alpha+2\gamma$ (donde hemos usado que $2\alpha+2\beta+2\gamma=180$). Como quiera que el enunciado nos dice que $\angle GID=2\beta$, se tiene en el triángulo $GID$ que $\angle IGD=180-2\beta-\alpha-2\gamma=\alpha$. Por lo tanto, los triángulos $GIC$ y $AIC$ son congruentes (tienen un lado en común y los ángulos adyacentes iguales). Esto nos dice que $A$ y $G$ son simétricos respecto de la bisectriz $CI$, luego $\angle FGI=\angle FAI=\alpha$ y concluimos que $\angle CGF=2\alpha$.
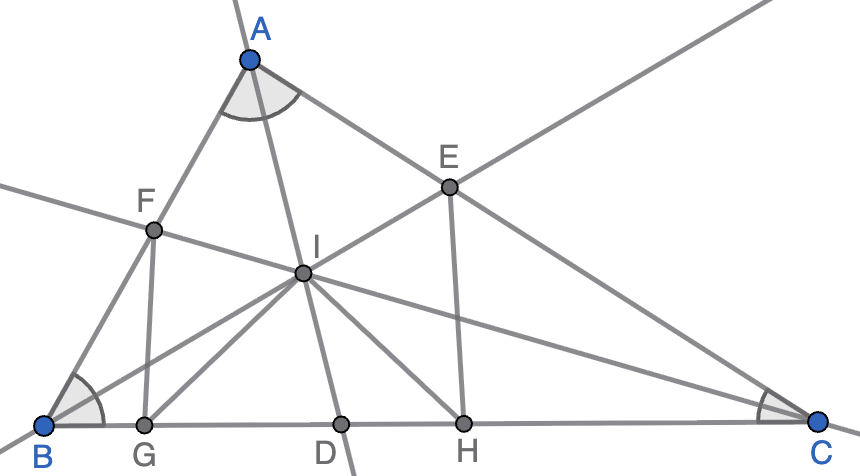
Está claro que los mismos argumentos funcionan para demostrar que $\angle DHE=\angle IHE=\alpha$, luego $\angle BHE=2\alpha$ y hemos terminado.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre