Olimpiadas de Matemáticas
Página de preparación y problemas
Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2434 problemas y 940 soluciones.
Problema 585
Sea $ABCD$ un cuadrilátero convexo tal que $AB\gt BC$, $CD = DA$ y $\angle ABD =\angle DBC$. Sea $E$ un punto de la recta $AB$ tal que $\angle DEB = 90^\circ$. Probar que $2AE = AB − BC$.
Sin pistas
Sin soluciones
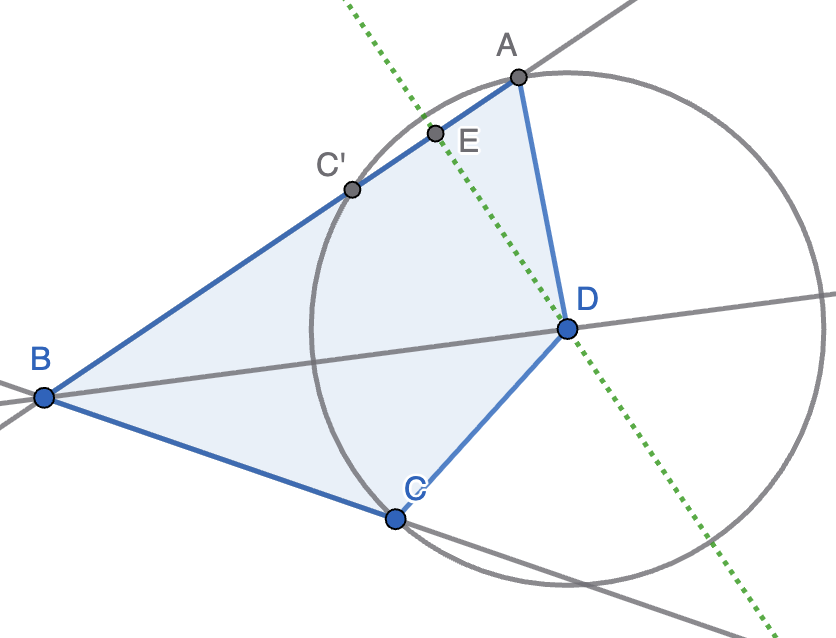
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2025. Esta página ha sido creada mediante software libre