Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 599
En la orilla de un río de $100$ metros de ancho está situada una planta eléctrica y en la orilla opuesta, a $500$ metros río arriba, se está construyendo una fábrica. Sabiendo que el río es rectilíneo entre la planta y la fábrica, que el tendido de cables a lo largo de la orilla cuesta $9$ euros cada metro y que el tendido de cables sobre el agua cuesta $15$ euros cada metro, ¿cuál es la longitud del tendido más económico posible entre la planta eléctrica y la fábrica?
pistasolución 1info
Pista. El camino más barato consistirá en ir en línea recta de la fabrica a un punto de la orilla opuesta y después en línea recta siguiendo la orilla hasta la planta eléctrica.
Solución. La situación es como se indica en la figura. Como dentro del mismo medio (agua o tierra) la menor distancia la realiza la línea recta, el camino óptimo recorrerá un trayecto rectilíneo en agua y otro rectilíneo en tierra (podemos suponer que el trayecto sobre el agua se realiza al principio sin perder generalidad). En cualquier caso, llamando a $x$ la distancia indicada en la figura, recorreremos $500-x$ en tierra y $\sqrt{10000+x^2}$ por agua según el teorema de Pitágoras. Dados los costes del enunciado, la función que nos da el coste total viene dada por
\[f(x)=9(500-x)+15\sqrt{10000+x^2}.\]
El mínimo de esta función se puede obtener haciendo $f'(x)=0$, pero vamos a razonar sin derivadas. Para ello, vamos a considerar la ecuación $f(x)=a$ para cierto valor $a$. Podemos desarrollar
\begin{align*}
f(x)=a&\ \Leftrightarrow\ 4500-9x-a=15\sqrt{10000+x^2}\\
&\ \Leftrightarrow\ (4500-9x-a)^2=225(10000+x^2).
\end{align*}
Desarrollando y usando la fórmula para la ecuación de segundo grado, tenemos que
\[x=\frac{3a-13500\pm 5\sqrt{18810000-9000a+a^2}}{48}.\]
Esta expresión nos dice que habrá valores de $x$ tales $f(x)=a$ si $18810000-9000a+a^2=(a-3300)(a-5700)\geq 0$. Como $a\leq 3300$ nos da valores negativos de $x$, deducimos de esta desigualdad que $a\geq 5700$, lo que nos da $x\geq 75$ para la solución de la ecuación de segundo grado con signo $+$. En definitiva, el valor mínimo ocurre para $x=75$ y su coste es $5700$ euros. Esto nos da una longitud (en metros) de
\[500-x+\sqrt{100^2+x^2}=425+\sqrt{100^2+75^2}=425+25\sqrt{4^2+3^2}=550.\]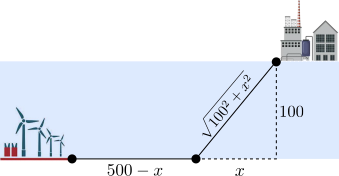

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre