Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 601
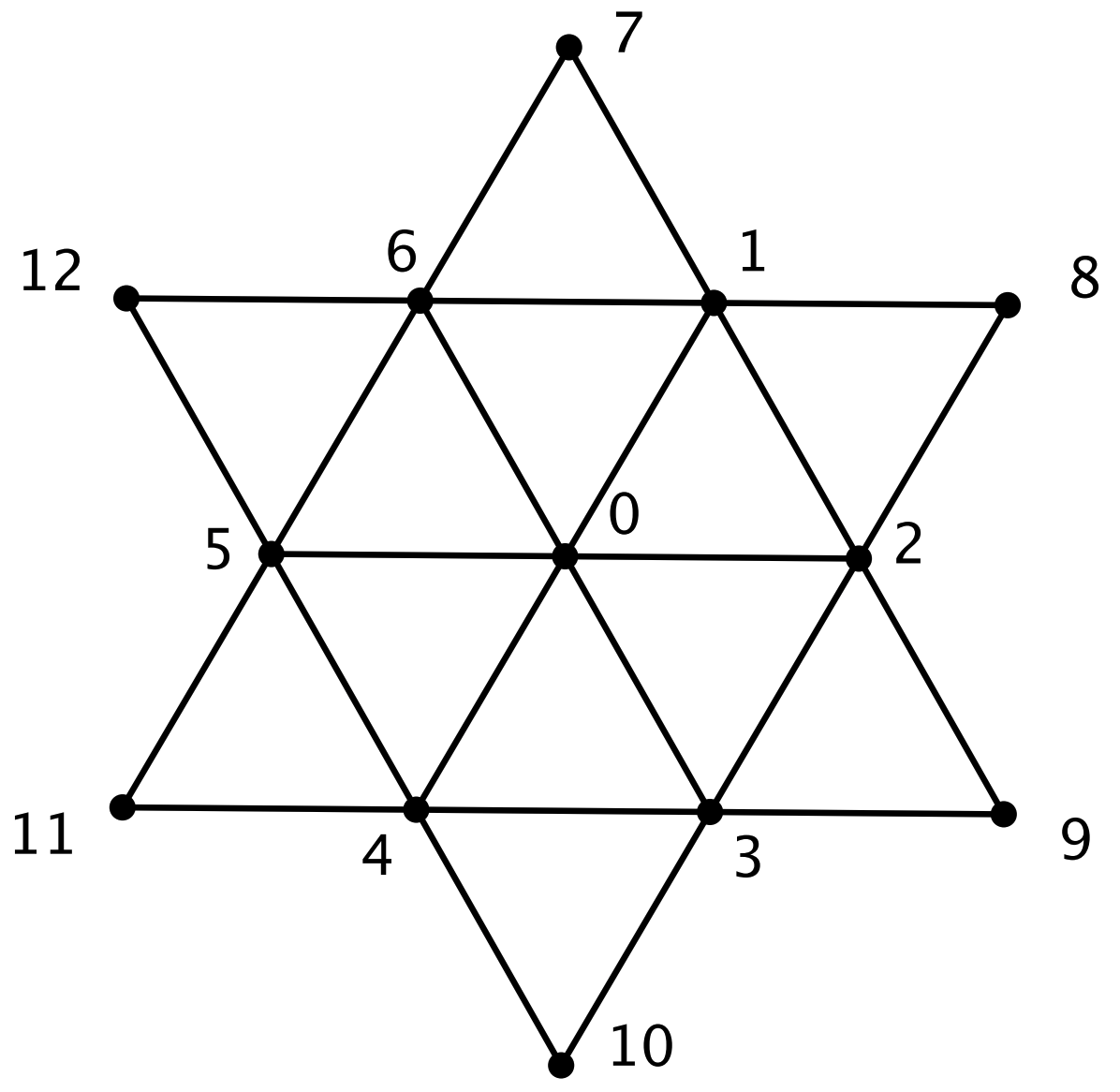
La estrella de seis puntas de la
figura es regular: todos los ángulos interiores de los triángulos pequeños son iguales. A cada uno de los trece puntos señalados se le asigna un color: verde o rojo. Demuestra que siempre habrá tres puntos del mismo color que son vértices de un triángulo equilátero.
pistasolución 1info
Pista. Fíjate en el triángulo de vértices $0,1,2$ y distingue casos según el color de sus vértices.
Solución. Tomemos el triángulo de vértices $0,1,2$ y supongamos que no tiene sus tres vértices del mismo color, luego tiene dos de un color (que supondremos es el verde) y otro del otro color (rojo). Tenemos dos casos, dependiendo de si los dos verdes son $0$ y $1$ o bien $1$ y $2$ (el caso en el que son $0$ y $2$ es simétrico).
- Si $0$ y $1$ son verdes, entonces $2$ y $6$ son rojos, luego $4$ es verde y $3$ y $5$ son rojos. En consecuencia, $9$ y $12$ son verdes y tenemos el triángulo equilátero de vértices $1,4,9$ con sus tres vértices verdes.
- Si $1$ y $2$ son verdes, entonces $0$ y $8$ son rojos, luego $7$ y $9$ son verdes. Por tanto, $3$, $4$, $5$, $6$ y $11$ son todos rojos y, en particular, el triángulo equilátero de vértices $3,6,11$ tiene todos sus vértices rojos.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre