Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 646
Sea $ABC$ un triángulo isósceles, con $AB = AC$. Sea $P$ un punto cualquiera del segmento $BC$ distinto de $B$ y $C$, y sea $N$ el punto medio de $AP$. Se construye un trapecio (convexo) $M_1M_2N_2N_1$, siendo $M_1$ el punto medio de $BP$, $M_2$ el punto medio de $PC$ y $M_1N_1$ y $M_2N_2$ perpendiculares a $BC$, tales que $N$, $N_1$ y $N_2$ están alineados. Demostrar que el área del trapecio es la mitad del área del triángulo dado.
pistasolución 1info
Pista. Demuestra que $N$ es el punto medio de $N_1N_2$.
Solución. Llamemos $Q$ al punto medio de $BC$ y $M$ al pie de la perpendicular desde $N$ al lado $BC$. Escribiremos por comodidad $a=BC$ y $x=BP$. Pongamos además, sin pérdida de generalidad, que $P$ está más cerca de $B$ que de $C$, es decir, que $x\leq\frac{a}{2}$. Como $M_1$ es el punto medio de $BP$, tenemos que $BM_1=M_1P=\frac{x}{2}$. Como $N$ es el punto medio de $AP$ y los segmentos $NM$ y $AQ$ son paralelos, el teorema de Thales nos dice que $PM=MQ=\frac{1}{2}(\frac{a}{2}-x)=\frac{a}{4}-\frac{x}{2}$. También tenemos que $QM_2=QC-M_2C=\frac{a}{2}-\frac{a-x}{2}=\frac{x}{2}$ y de todo esto deducimos que
\begin{align*}
M_1M&=M_1P+PM=\frac{x}{2}+\left(\frac{a}{4}-\frac{x}{2}\right)=\frac{a}{4},\\
MM_2&=MQ+QM_2=\left(\frac{a}{4}-\frac{x}{2}\right)+\frac{x}{2}=\frac{a}{4}.
\end{align*}
Obtenemos así que $M$ es el punto medio de $M_1M_2$. El área del trapecio es la base media $MN$ (que es igual a $\frac{AQ}{2}$ por el mismo teorema de Thales anterior) por la altura $M_1M_2=\frac{a}{2}$, luego $M_1M_2N_2N_1$ tiene área $\frac{1}{2}(\frac{a\cdot AQ}{2})$, que es claramente la mitad del área de $ABC$.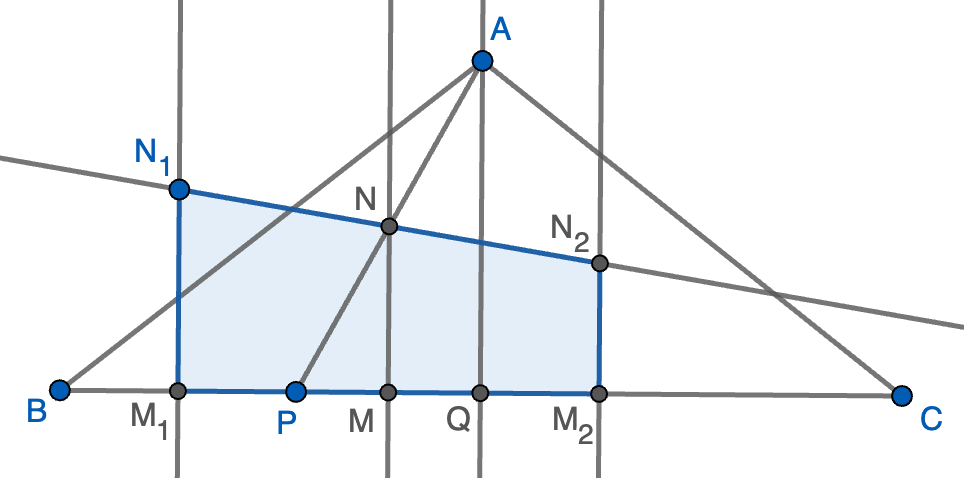

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre