Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 664
OIM, 1991-P6
Dados tres puntos no alineados $M$, $N$ y $P$, construir un triángulo sabiendo que $M$ y $N$ son los puntos medios de dos de sus lados y que $P$ es el punto de intersección de sus alturas.
pistasolución 1info
Pista. Considera un paralelogramo $APBX$ si $M$ es el punto medio de $AB$.
Solución. Renombraremos el punto $P$ como $H$, ya que se trata del ortocentro del triángulo. Supongamos que el triángulo $ABC$ ya está construido para tener intuición sobre cómo hacer la cosntrucción. Supongamos que $M$ es el punto medio de $AB$ y $N$ es el punto medio de $AC$. Si consideramos un punto $X$ tal que $AHBX$ es un paralelogramo, entonces $AX$ es paralela a $BH$ (que es una altura del triángulo) y, por tanto, perpendicular a $AC$. Por tanto, el triángulo $XAN$ es rectángulo en $A$ y $A$ debe estar sobre la circunferencia de diámetro $XN$. Por otro lado $A$ también debe estar en la perpendicular a $MN$ que pasa por $H$ (que es la altura del lado $A$). Esto nos permite determinar el punto $A$, a partir del cual se obtienen $B$ y $C$ rápidamente. El proceso de construcción es el siguiente (la construcción en cada paso es sencilla y se deja como ejercicio entender cómo se haría con regla y compás):
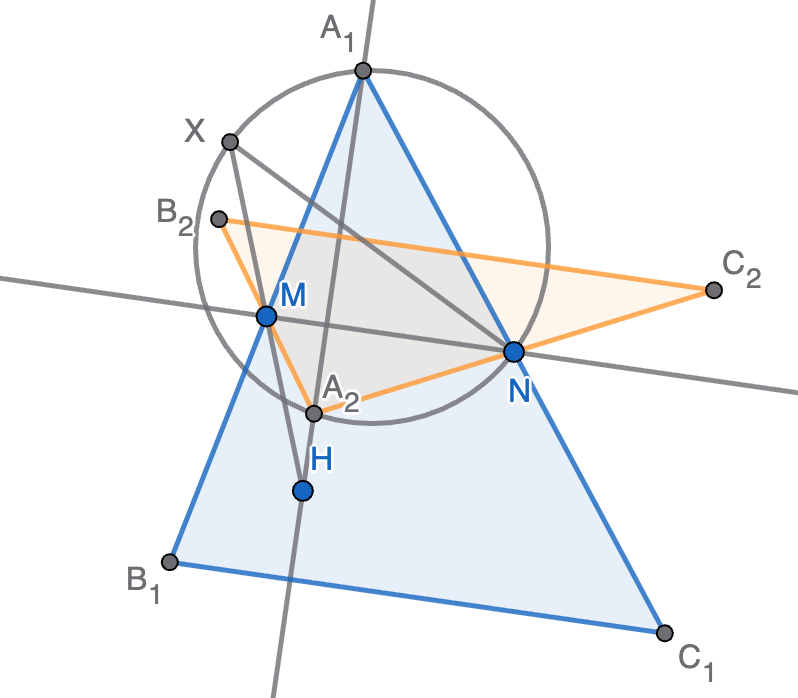
- Se determina el punto $X$ tal que $M$ es el punto medio de $XH$.
- Se traza la circunferencia de diámetro $XN$.
- Se ubica el vértice $A$ en la intersección de dicha circunferencia con la perpendicular a $MN$ que pasa por $H$.
- Se determinan los puntos $B$ y $C$ de forma que $M$ es el punto medio de $AB$ y $N$ es el punto medio de $AN$.
Ahora bien, puede ocurrir que la intersección de la recta y la circunferencia sea vacía, tenga un único punto o tenga dos puntos. Por el argumento previo, esto se corresponderá con que haya 0, 1 o 2 soluciones al problema. Se muestra en la figura un ejemplo en el que hay dos soluciones $A_1B_1C_1$ (en azul) y $A_2B_2C_2$ (en naranja).

Nota. Sería interesante (como nuevo ejercicio), hallar condiciones sencillas sobre $M$, $N$ y $H$ para que exista solución.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre