Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Consideremos la circunferencia $\Gamma'$ que surge al trasladar $\Gamma$ una distancia $h$ en vertical. El problema equivale a encontrar una recta horizontal que corte a $\Gamma$ y $\Gamma'$ en sendos segmentos cuya suma de longitudes sea precisamente $m$ (el segmento correspondiente a $\Gamma$ es una de las bases del trapecio y el segmento correspondiente a $\Gamma'$ será la otra base después de trasladarlo $-h$ en vertical.

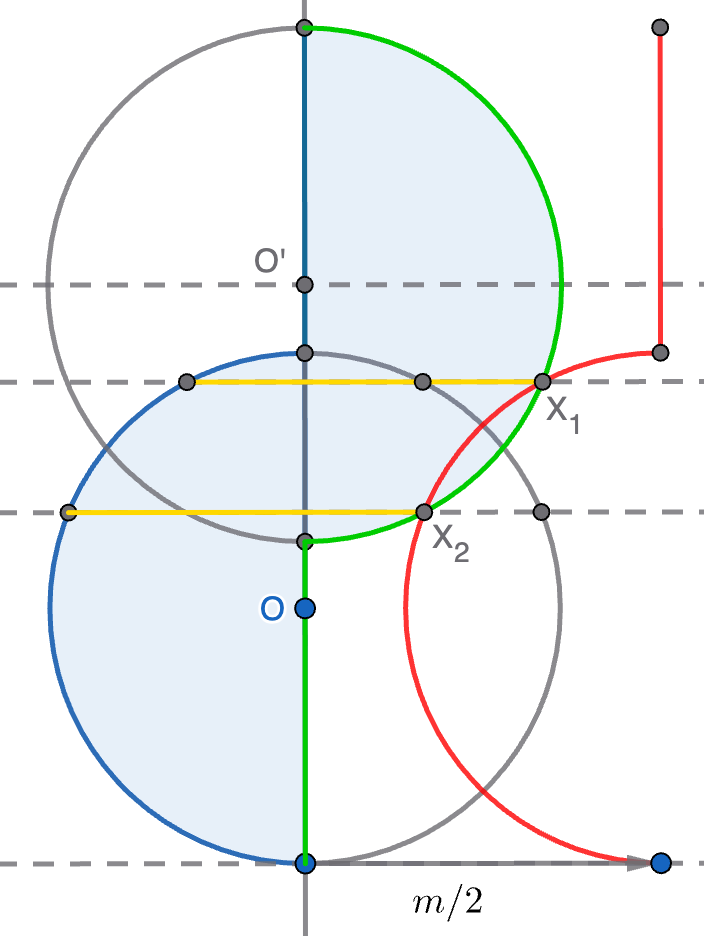
Consideremos entonces el eje de simetría vertical común a ambas circunferencias y nos quedamos con la semicircunferencia $S$ de $\Gamma$ a la derecha del eje y con la semicircunferencia $S'$ de $\Gamma'$ a la derecha del eje, delimitando ambas la región sombreada de la figura. Como nos hemos quedado con la mitad de cada circunferencia, ahora queremos ver qué recta horizontal corta a la zona sombreada en una longitud $\frac{m}{2}$. Para ello, movemos la figura $\frac{m}{2}$ a la derecha y vemos dónde corta el borde izquierdo trasladado (en rojo en la figura) al borde derecho original (en verde). Cada punto $X$ en la intersección nos da una posible solución que viene dada por la recta horizontal que pasa por $X$. En la figura se ha puesto un ejemplo en el que hay dos soluciones $X_1$ y $X_2$ que producen sendos segmentos de longitud $\frac{m}{2}$, indicados en amarillo.