Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 689
Dibuja una semicircunferencia con centro en $O$ y diámetro $AB$ y, en su interior, otra, con diámetro $OA$. Traza por un punto $C$ de $OA$ una recta perpendicular a dicho segmento $OA$, que cortará a la semicircunferencia pequeña en $D$ y a la grande en $E$ y, finalmente, la recta $AD$ que cortará al semicírculo grande en $F$. Demuestra que la circunferencia circunscrita al triángulo $DEF$ es tangente a la cuerda $AE$ en $E$.
pistasolución 1info
Pista. Demuestra que $AD\cdot AF=AE^2$.
Solución. La circunferencia circunscrita al triángulo $DEF$ será tangente a la cuerda $AE$ cuando $AD\cdot AF=AE^2$ usando la potencia del punto $A$ respecto de dicha circunferencia. Ahora bien, una homotecia de centro $A$ y razón $2$ transforma la semicircunferencia pequeña en la grande y transforma $D$ en $F$, de donde se deduce que $AF=2AD$. Esto nos dice que el problema equivale a demostrar que $2AD^2=AE^2$.
Pongamos $x=AC$ y $r=AO$. Entonces, $CO=r-x$ y el teorema de la altura en el triángulo rectángulo $ADO$ nos dice que $CD^2=AC\cdot CO=x(r-x)$, de donde $AD^2=AC^2+CD^2=x^2+x(r-x)=rx$ por el teorema de Pitágoras. De forma similar, en el triángulo rectángulo $AEO$, el teorema de la altura nos dice que $CE^2=AC\cdot CB=x(2r-x)$, luego
\[AE^2=AC^2+CE^2=x^2+x(2r-x)=2xr=2AD^2,\]
como queríamos probar.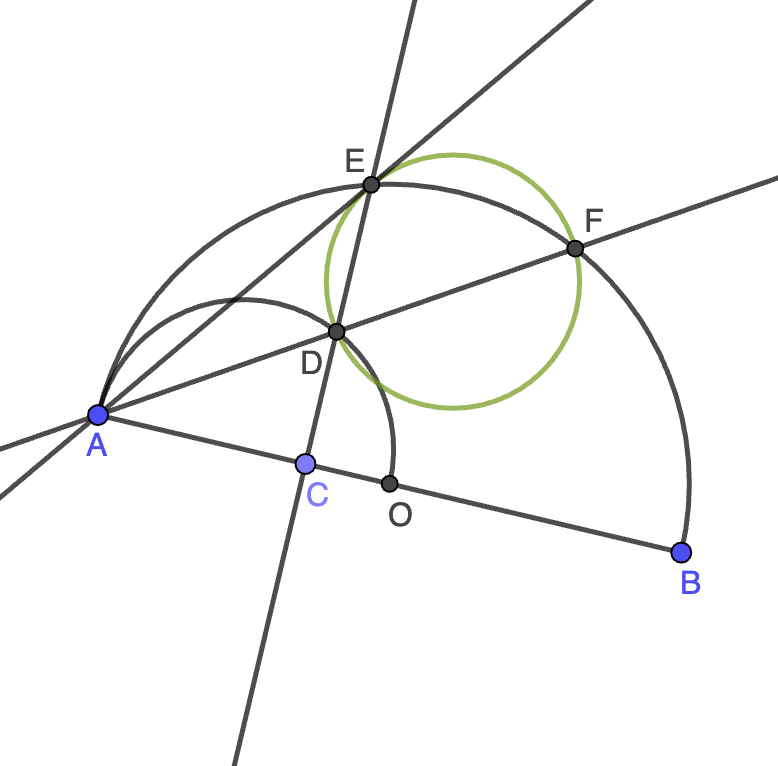
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre