Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 690
¿Cuál es el número máximo de vértices que podemos elegir de un polígono regular de 21 lados para que, al trazar los segmentos que los unen entre sí, no haya dos con la misma longitud?
pistasolución 1info
Pista. Encuentra 5 vértices tales que todos los segmentos que definen tienen distintas distancias.
Solución. En un polígono regular de 21 lados hay 10 distancias posibles entre vértices ya que los 20 segmentos que salen de un vértice concreto tienen longitudes iguales por parejas simétricas. Por tanto, si elegimos $n\geq 6$ o más vértices, tendremos $\binom{n}{2}\geq\binom{6}{2}=15$ segmentos entre ellos y la respuesta será negativa. La pregunta es si se puede con 5 vértices, que definen justamente $\binom{5}{2}=10$ segmentos, es decir, ¿existen 5 vértices del 21-ágono regular tales que todas sus distancias son distintas? La respuesta es que sí, como se muestra en la figura.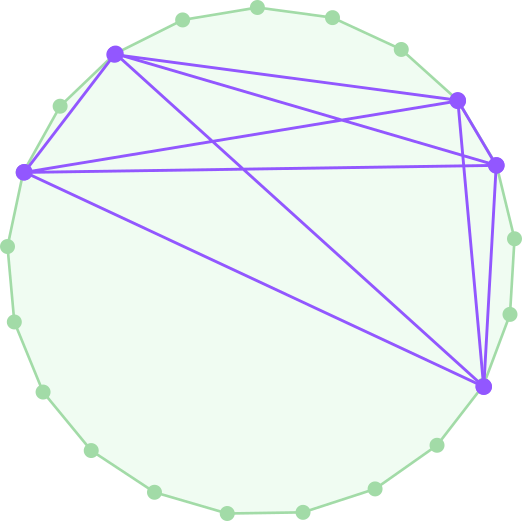

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre