Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 698
OME Local, 2003-P12
Por turnos y en orden alfabético según sus nombres, tres amigos lanzan un dado. Quien saque un 6 en primer lugar gana lo apostado. Por cada euro que apueste Carlos, ¿qué cantidad han de poner Ana y Blas para equilibrar el juego y lograr que sea equitativo, es decir, para que las expectativas de ganancia sean las mismas para los tres colegas y no se vean afectadas por el orden de actuación al lanzar el dado?
pistasolución 1info
Pista. Si llamamos $p_{X,Y}$ a la probabilidad de que gane el jugador $X$ el juego cuando $Y$ está tirando los dados, obtenemos 9 probabilidades desconocidas. Usa la dinámica del juego para establecer tres sistemas de ecuaciones lineales que relacionen estás probabilidades y luego resuélvelos. Observa que para que el juego sea equitativo, las apuestas iniciales deben ser proporcionales a las probabilidades de ganar.
Solución. Vamos a denotar por $p_{X,Y}$ a la probabilidad de que gane el jugador $X$ cuando va a hacer su tirada el jugador $Y$. Observamos que cuando tira un jugador, tiene una probabilidad de ganar directamente $\frac{1}{6}$ y los otros $\frac{5}{6}$ son su probabilidad de ganar una vez le toca al siguiente. De esta forma, tenemos los siguientes tres sistemas de ecuaciones lineales para las nueve probabilidades que desconocemos:
\[\left\{\begin{array}{l}p_{A,A}=\frac{1}{6}+\frac{5}{6}p_{A,B}\\p_{A,B}=\frac{5}{6}p_{A,C}\\p_{A,C}=\frac{5}{6}p_{A,A}\end{array}\right.\quad
\left\{\begin{array}{l}p_{B,A}=\frac{5}{6}p_{B,B}\\p_{B,B}=\frac{1}{6}+\frac{5}{6}p_{B,C}\\p_{B,C}=\frac{5}{6}p_{B,A}\end{array}\right.\quad
\left\{\begin{array}{l}p_{C,A}=\frac{5}{6}p_{C,B}\\p_{C,B}=\frac{5}{6}p_{C,C}\\p_{C,C}=\frac{1}{6}+\frac{5}{6}p_{C,A}\end{array}\right.\]
Esto responde al diagrama indicado en la figura más abajo. En realidad, los tres sistemas lineales son el mismo (renombrando las incógnitas) y se pueden resolver fácilmente:
\[\left\{\begin{array}{l}p_{A,A}=\frac{36}{91}\\p_{A,B}=\frac{25}{91}\\p_{A,C}=\frac{30}{91}\end{array}\right.\qquad
\left\{\begin{array}{l}p_{B,A}=\frac{30}{91}\\p_{B,B}=\frac{36}{91}\\p_{B,C}=\frac{25}{91}\end{array}\right.\qquad
\left\{\begin{array}{l}p_{C,A}=\frac{25}{91}\\p_{C,B}=\frac{30}{91}\\p_{C,C}=\frac{36}{91}\end{array}\right.\]
Al empezar jugando $A$ la probabilidad que tiene de ganar es $\frac{36}{91}$, mientras que la probabilidad de $B$ es $\frac{30}{91}$ y la de $C$ es $\frac{25}{91}$. Si Carlos apuesta 1€, entonces Blas tiene que apostar $\frac{30}{25}=1.2$€ y Ana tiene que apostar $\frac{36}{25}=1.44$€ (la apuesta tiene que ser proporcional a la probabilidad de ganar si queremos que el juego sea equitativo).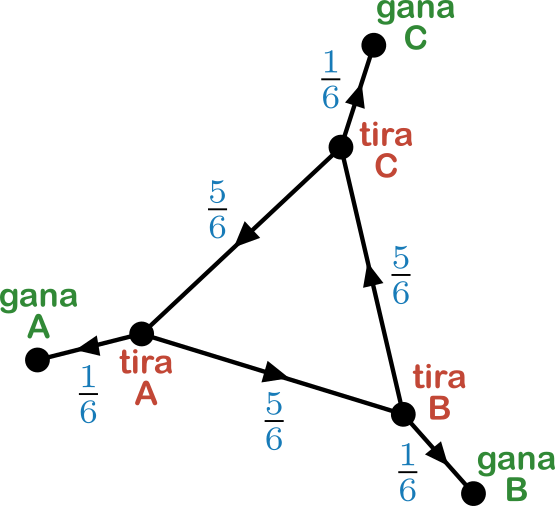

Nota. Este esquema para calcular probabilidades, aunque puede parecer sofisticado, es un método establecido en matemáticas conocido como cadenas de Markov. Si quisiéramos hacer un árbol con todas las posibilidades, sería infinito ya que podría ocurrir que nunca nadie saque un $6$. De esta manera, se entiende mucho mejor la logística del juego.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre