Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
- Dos elementos de $S$ pertenecen simultáneamente a exactamente uno de los subconjuntos.
- Dos subconjuntos cualesquiera tienen intersección no vacía (y, por tanto, formada por un único elemento por (a)).
Veamos en primer lugar que esto resuelve el problema original. Para cada elemento de $a\in S$, cada uno de los $p^2+p=(p+1)p$ elementos restantes de $S$ tiene que estar en un único subconjunto que también contenga a $a$, lo que nos fuerza a que haya exactamente $p+1$ subconjuntos que contengan a $a$ y esto prueba que en cada columna de la tabla habrá exactamente $k=p+1$ elementos. Además, esta configuración es óptima, ya que al haber exactamente $p+1$ subconjuntos que contienen a cada $a\in S$, iterando sobre todos los $a\in S$ tendremos un total de $(p^2+p+1)(p+1)$ subconjuntos, cada uno contado $p+1$ veces (una por cada uno de sus elementos), lo que nos dice que el número de subconjuntos debe ser $p^2+p+1$.
El mejor modelo de subconjuntos tales dos elementos cualesquiera definen exactamente uno de los subconjuntos lo dan las rectas del plano: dos puntos definen una única recta que pasa por ellos. Vamos a hacer lo mismo pero en un conjunto de $p$ elementos, para lo que vamos a trabajar en lo que sigue con puntos de coordenadas enteras módulo el primo $p$. Concretamente, consideraremos los $p^2$ puntos $(x,y)$ que cumplen $0\leq x,y\lt p$ (luego añadiremos los $p+1$ puntos restantes para que las rectas paralelas también se corten en algún punto, la otra condición que buscamos). Las rectas módulo $p$ son los subconjuntos dados por una ecuación $ax+by\equiv c\ (\text{mod }p)$ siendo $0\leq a,b,c\lt p$ y $a$ y $b$ no ambos nulos. Hay dos tipos de rectas:
- Verticales. Se obtienen para $b\equiv 0$, luego $a\not\equiv 0$ y podemos despejar $x\equiv a^{-1}c$ (siendo $a^{-1}$ el inverso de $a$ módulo $p$). Por tanto, las podemos escribir como $x\equiv n$ para algún $0\leq n\lt p$.
- No verticales. Si $b\not\equiv 0$, podemos despejar $y\equiv b^{-1}c-b^{-1}ax$. Las podemos escribir como $y\equiv mx+n$ para ciertos $0\leq m,n\lt p$.
Por ejemplo, en la imagen, hemos dibujado las rectas clasificadas según su pendiente para $p=5$ y los distintos colores corresponden a cambiar $n$. Veamos algunas propiedades:
- Cada recta tiene exactamente $p$ elementos. Por un lado, la recta vertical $x\equiv n$ tiene a los $p$ elementos $(n,y)$ para $0\leq y\lt p$. Por otro lado, la recta no vertical $y\equiv mx+n$ tiene también $p$ puntos, uno para cada elección $0\leq x\lt p$ ya que sólo hay que calcular $y$, que está despejado.
- Dos rectas se cortan en un único punto salvo que sean paralelas. En efecto, el sistema formado por dos rectas verticales distintas es incompatible (son paralelas), al igual que el formado por dos rectas no verticales de la misma pendiente. Si tomamos una vertical y una no vertical o bien dos no verticales con distinta pendiente, el sistema se puede resolver fácilmente módulo $p$ y tenemos una única solución.
- Dada una recta, hay exactamente $p$ rectas paralelas a ella (incluyéndo a la propia recta), lo que nos da un total de $p(p+1)$ rectas. Observemos que $p^2$ de ellas son no verticales (según elección de $0\leq m,n\lt p$ y hay $p$ para cada pendiente) y las $p$ restantes son las verticales.
Con todo esto en mente, vamos a añadir $p+1$ elementos adicionales $P_0,P_1,\ldots,P_p,P_v$ a nuestro plano: a cada recta de ecuación $y\equiv m+nx$ le añadimos el $P_m$, según su pendiente, y a cada recta $x\equiv m$ le añadimos $P_v$. De esta forma, rectas paralelas tienen un punto adicional común y obtenemos $p(p+1)$ rectas con $p+1$ puntos cada una. Nos falta definir una última recta: la formada por los puntos $P_0,P_1,\ldots,P_p,P_v$. Es inmediato comprobar que estos $p^2+p+1$ subconjuntos cumplen las condiciones (a) y (b) propuestas y esto demuestra el enunciado.
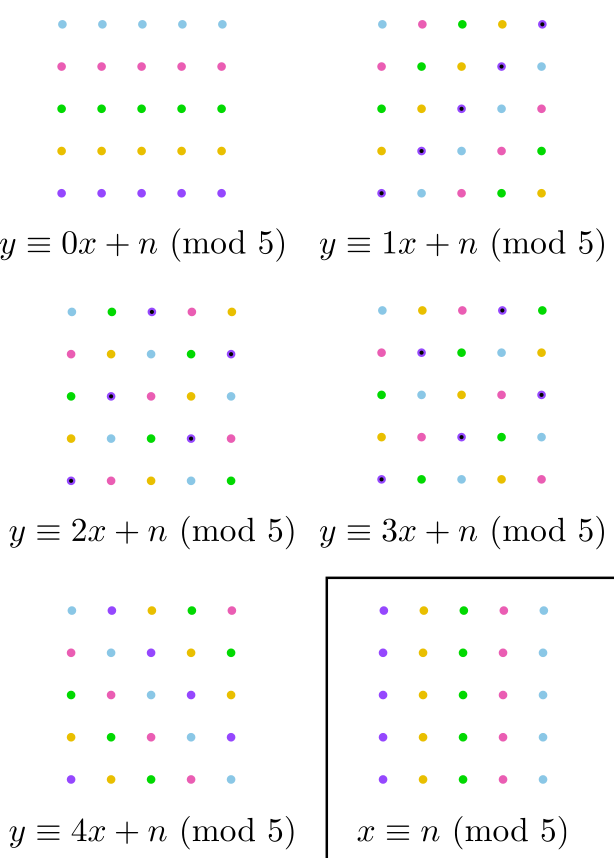
Nota. Aunque parezca increíblemente sofisticado, lo que se hace en la solución no es otra cosa que construir el plano proyectivo sobre un cuerpo de $p$ elementos. Las rectas afines o proyectivas sobre cuerpos finitos dan multitud de ejemplos con interesantes propiedades combinatorias.
Informar de error en enunciado Informar de procedencia del problema