Administración     

Olimpiadas de Matemáticas
Página de preparación y problemas

OME Local
OME Andaluza
OME Nacional
OIM
IMO
EGMO
USAMO
ASU
OMCC
Retos UJA
Selector
La base de datos contiene 2434 problemas y 940 soluciones.
Problema 713
OIM, 1996-P5
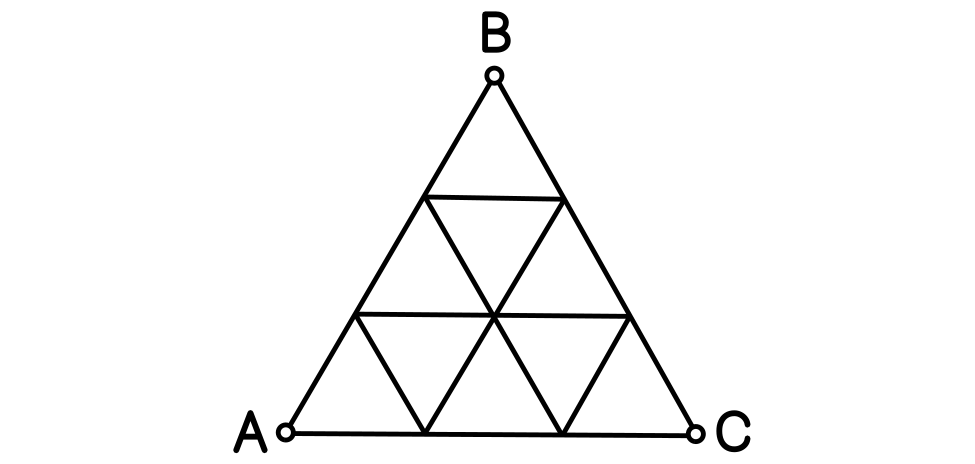
Tres fichas $A$, $B$ y $C$ están situadas una en cada vértice de un triángulo equilátero de lado $n$. Se ha dividido el triángulo en triangulos equiláteros más pequeños de lado $1$ (la figura muestra el caso $n = 3$). Inicialmente, todas las líneas de la figura están pintadas de azul. Las fichas se desplazan por líneas, pintando de rojo su trayectoria, de acuerdo con las dos reglas siguientes:
  • Primero se mueve $A$, después $B$ y después $C$, después $A$, y así sucesivamente, por turnos. En cada turno cada ficha recorre un lado de un triángulo pequeño, de un extremo a otro.
  • Ninguna ficha puede recorrer un lado de un triángulo pequeño que ya esté pintado en rojo, pero puede descansar en un extremo pintado, incluso si ya hay otra ficha esperando allí su turno.
Demostrar que, para todo entero $n\gt 0$, es posible pintar de rojo todos los lados de todos los triángulos pequeños.
imagen
pistasolución 1info
Pista. Descompón el grafo en tres grafos eulerianos con el mismo número de aristas. Se puede hacer de forma que cada uno de estos tres grafos sea una rotación de $120^\circ$ de los otros dos, es decir, manteniendo el centro de simetría.
Solución. La figura (para $n=3$) tiene 18 aristas que se pueden agrupar en 6 triángulos equiláteros de lado 1 (con orientación $\triangle$) o bien, si previamente quitamos los lados del triángulo grande, quedan 9 aristas que se agrupan en tres triángulos (con orientación $\bigtriangledown$). Para el caso de $n$ general, tenemos $\frac{n(n+1)}{2}$ triángulos de tipo $\triangle$ y $\frac{n(n-1)}{2}$ triángulos de tipo $\bigtriangledown$ (tras eliminar los lados grandes). Vamos a distinguir dos casos:
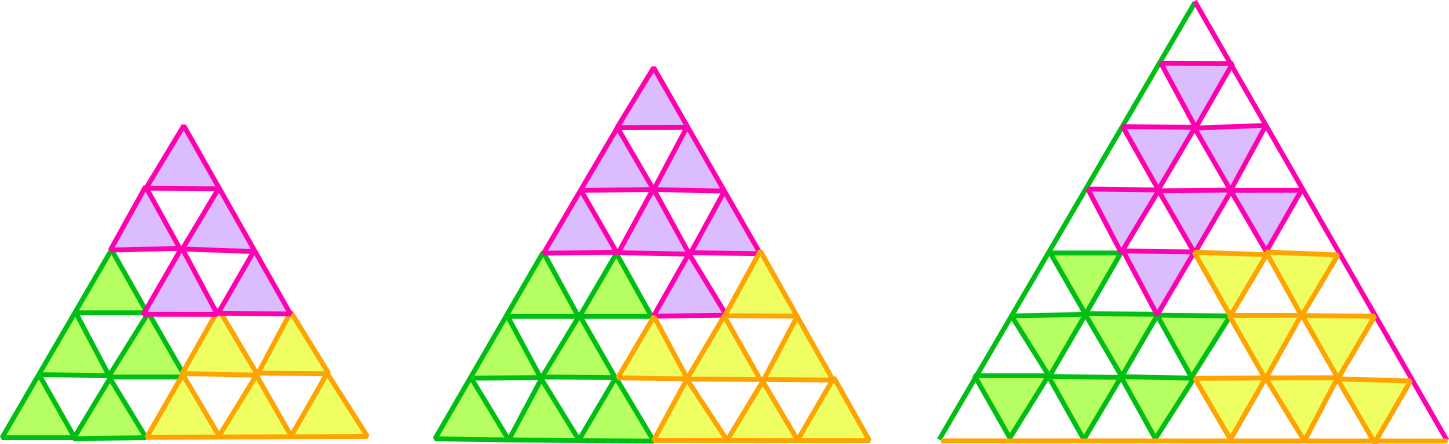
  • Si $n$ es de la forma $3k$ o $3k+2$, entonces el número de triángulos de tipo $\triangle$ es múltiplo de $3$. Los dividimos en tres subconjuntos que de forma que en cada subconjunto haya el mismo número $m$ de triángulos, estén conectados entre sí a través de vértices y en un subconjunto esté el vértice $A$, en otro el $B$ y en otro el $C$ (ver la nota). Las aristas de tales triángulos forman un grafo tal que en cada vértice hay un número par de aristas (cada triángulo aporta dos aristas en cada vértice). Por tanto, usando el teorema de Euler para grafos, partiendo de $A$ hay un camino de longitud $3m$ que empieza y acaba en $A$ y lo mismo con $B$ y $C$.
  • Si $n$ es de la forma $3k+1$, hay una cantidad de triángulos $\bigtriangledown$ que es múltiplo de $3$, luego repartimos el segmento $AB$ para $A$, el segmento $BC$ para $B$ y el segmento $CA$ para $C$. Ahora los triángulos $\bigtriangledown$ los dividimos en tres subconjuntos al igual que en el caso anterior, pero en este caso conectados con los segmentos correspondientes a los jugadores. De esta manera, los lados de los $m$ triangulitos $\bigtriangledown$ asignados a cada jugador junto con el lado grande forman un grafo euleriano en el que todos los vértices tienen un número par de aristas menos los extremos del lado grande. Por tanto, existen caminos disjuntos de longitud $3m+n$ que van de $A$ a $B$, de $B$ a $C$ y de $C$ a $A$, respectivamente.

En la figura se pueden ver ejemplos de los caminos propuestos para $n=5$, $n=6$ y $n=7$, donde se han usado colores distintos para cada jugador y se han coloreado los triangulitos $\triangle$ y $\bigtriangledown$ asignados.

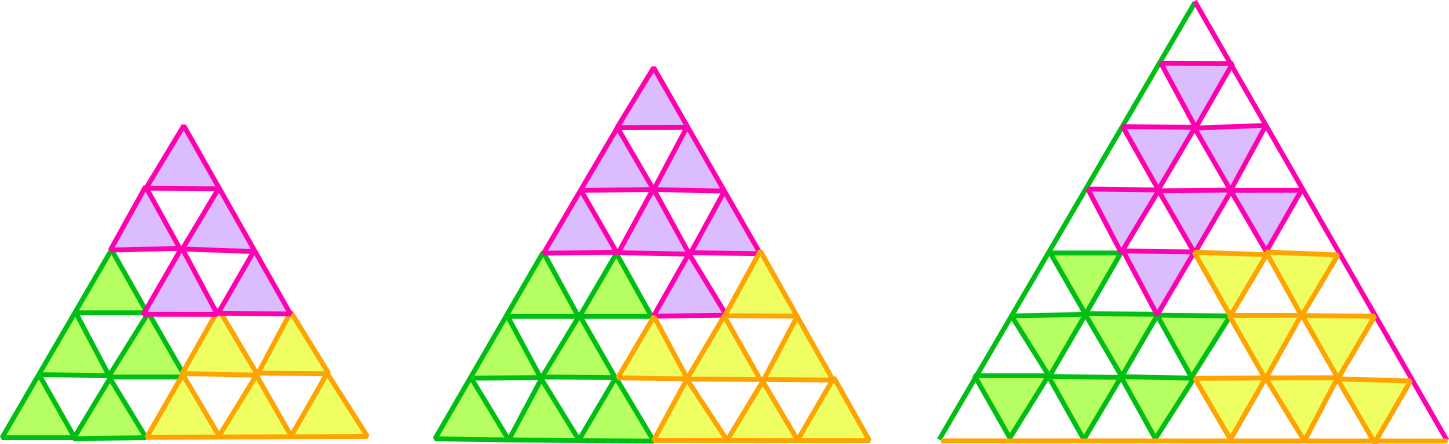
imagen

Nota. No se ha dicho realmente cómo se asignan los triángulos $\triangle$ y $\bigtriangledown$ y en realidad hay muchas formas de hacerlo manteniendo la conexión del territorio de cada jugador. Una forma práctica de asignar es darle a cada jugador el triángulo más cercano a su vértice (caso $n=3k$ o $n=3k+2$) o a su lado (caso $n=3k+1$) y repartir aquellos triángulos que equidistan de dos jugadores de forma simétrica (no hay ninguno que equidiste de los tres jugadores en ninguno de los dos casos).

Informar error
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2025. Esta página ha sido creada mediante software libre