Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 720
Sea $M$ un punto interior del segmento $AB$. Se construyen cuadrados $AMCD$ y $BEHM$ en el mismo lado de $AB$. Sea $N$ el punto de intersección (distinto de $M$) de las circunferencias circunscritas a dichos cuadrados.
- Probar que los puntos $B$, $N$ y $C$ están alineados.
- Probar que el punto $H$ es el ortocentro del triángulo $ABC$.
pistasolución 1info
Pista. ¿Qué relación hay entre los triángulos $AMH$ y $CMB$?
Solución. Los dos triángulos $AHM$ y $CMB$ son congruentes por ser rectángulos y tener los catetos iguales (son iguales a los lados de los cuadrados). Además, podemos pasar de $AHM$ a $CMB$ mediante una rotación de $90^\circ$ con centro en $M$, luego la recta $AH$ (en rojo discontinuo) es perpendicular a $BC$. Ahora bien, la recta $BC$ también es perpendicular a $AN$ ya que $AC$ es un diámetro de la circunferencia circunscrita al cuadrado $AMCD$. Por tanto $AN$ y $AH$ son la misma recta, es decir, $A$, $H$ y $N$ están alineados. Respondemos ahora a las dos cuestiones:
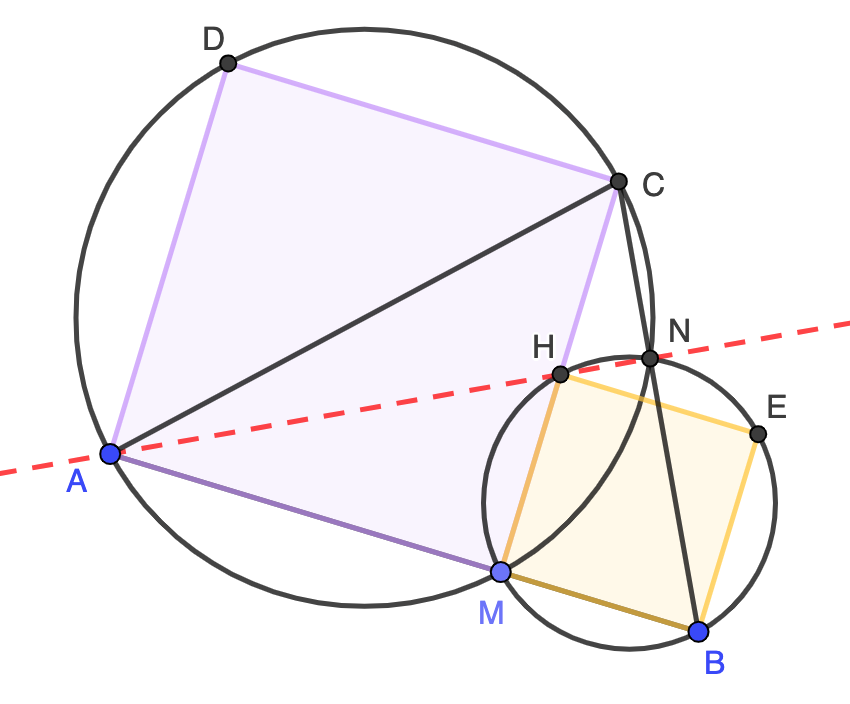
- El ángulo $\angle HNB$ es recto ya que $HB$ es un diámetro de la circunferencia circunscrita al cuadrado $MBEH$. Por tanto, tanto $\angle HNB$ como $\angle HNC$ son rectos, lo que nos dice que $B$, $N$ y $C$ están alineados.
- Con lo ya demostrado, tenemos que $AN$ es la altura que pasa por $A$ en el triángulo $ABC$ y es obvio que $CM$ es la altura que pasa por el vértice $C$. Su intersección es $H$ y, por consiguiente, $H$ es el ortocentro de $ABC$.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre