Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 733
Se dan 16 puntos formando una cuadrícula como en la figura, donde se han destacado dos esquinas opuestas $A$ y $D$. Se fijan otros dos puntos $B$ y $C$ con la condición de que las seis distancias determinadas por los cuatro puntos $A,B,C,D$ sean distintas.
- ¿Cuántas figuras de 4 puntos existen con estas condiciones del enunciado?
- ¿Cuántas de ellas son geométricamente distintas (es decir, que no se deducen de otras por simetría)?
- Si representamos en coordenadas enteras según la cuadrícula $A=(x_1,y_1)=(1,1)$, $B=(x_2,y_2)$, $C=(x_3,y_3)$ y $D=(x_4,y_4)=(4,4)$, razonar que la suma \[\sum_{i,j=1}^4\left(|x_i-x_j|+|y_i-y_j|\right)\] es la misma para cualquiera de tales configuraciones de puntos $A,B,C,D$.

pistasolución 1info
Pista. Solo hay 3 formas de colocar el vértice $B$ salvo simetría de la figura. Analiza las posibles posiciones de $C$ para cada una de ellas.
Solución. Observemos que $B$ y $C$ no pueden estar sobre la diagonal que no contiene a $A$ y $D$ (esta diagonal es la mediatriz de $AD$). Esto nos deja, salvo simetría respecto de alguna de las diagonales, solo tres posibles posiciones para $B$, que dan lugar a los tres casos que se muestran en la figura. Para cada uno de ellos se han marcado con una cruz roja las posiciones prohibidas para $C$ ya que incumplirían la condición de las distancias distintas. Es un poco laborioso no dejarse ningún caso, pero factible si se procede de forma ordenada.
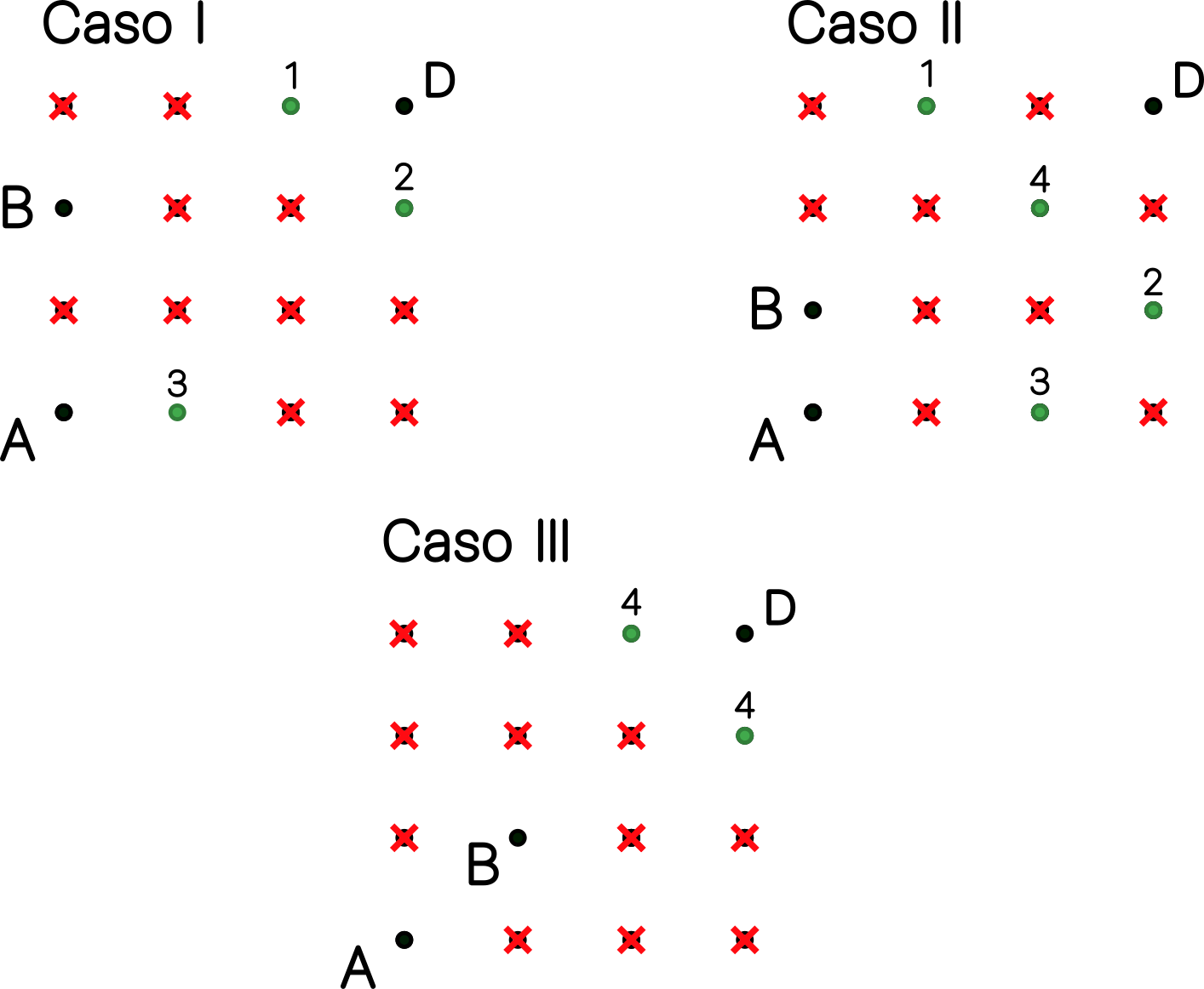
- En el caso I, hay 3 posiciones para $C$; como hay 4 posiciones de $B$ que producen el caso 1, tenemos un total de 12 configuraciones. En el caso II, hay 4 posiciones para $C$ para cada una de las cuatro posiciones para $B$, lo que nos da 16 configuraciones. En el caso III, tenemos 2 posiciones para C para cada una de las dos posiciones para $B$, lo que nos da 4 configuraciones. Tenemos así un total de $12+16+4=32$ configuraciones distintas de los puntos $B$ y $C$, que es la respuesta a (a).
- Para ver las que se obtienen salvo simetría, podemos restringirnos a las posiciones de $B$ de la figura. Ahora bien, se han marcado con números del 1 al 4 las posiciones de $C$ donde posiciones que comparten número son simétricas. Esto nos da la respuesta $4$ al apartado (b), ver la nota.
- Como los movimientos rígidos que estamos considerando conservan la cuadrícula, sólo habrá que analizar las configuraciones 1 a 4 dadas en el apartado (b) y ver que en todas ellas la suma $S$ del enunciado es la misma:
- Configuración 1: $S=2(1+3+3+2+2+0+2+3+3+1+1+0)=42$.
- Configuración 2: $S=2(2+2+3+0+1+1+0+3+3+3+3+0)=42$.
- Configuración 3: $S=2(0+2+3+2+3+1+0+1+3+1+3+2)=42$.
- Configuración 4: $S=2(1+2+3+1+2+1+1+3+3+2+2+0)=42$.

Nota. En el apartado (b) se ha considerado que dos conjuntos de 4 puntos son simétricos si se puede pasar de uno al otro por movimientos rígidos. A posteriori, se ha visto que la solución oficial contempla que el movimiento rígido conserve la etiqueta $A,B,C,D$ de los puntos, en cuyo caso hay 8 configuraciones.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre