Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 737
El ángulo $A$ del triángulo isósceles $ABC$ mide $36^\circ$, siendo iguales sus ángulos $B$ y $C$. La bisectriz de su ángulo $C$ corta al lado opuesto en el punto $D$.
- Calcular las medidas de los ángulos del triángulo $BCD$.
- Expresar la medida del lado $BC$ en función de la medida del lado $AC$, sin que en la expresión aparezcan razones trigonométricas.
pistasolución 1info
Pista. Busca un triángulo semejante a $ABC$ en la figura que resulta al trazar las diagonales de un pentágono regular.
Solución. Por ser el triángulo isósceles, tenemos que $\angle ABC=\angle ACB=\frac{180-36}{2}=72^\circ$. La bisectriz divide al ángulo en dos ángulos iguales, luego $\angle ABD=\angle DBC=\frac{72}{2}=36^\circ$. Además, como la suma de los ángulos de $BCD$ es $180^\circ$, obtenemos rápidamente $\angle BDC=180-36-72=72$. Por tanto, el triángulo $BCD$ es isósceles y tiene ángulos de $36^\circ, 72^\circ, 72^\circ$ (véase la figura).
El triángulo $ABD$ también es isósceles por tener dos ángulos iguales a $36^\circ$, luego $BC=BD=AD$. Además, $BCD$ y $ABC$ son semejantes por tener los ángulos iguales, luego
\[\frac{AC}{BC}=\frac{BC}{CD}=\frac{BC}{AC-AD}=\frac{BC}{AC-BC}.\]
De esta igualdad, obtenemos que $AC^2-AC\cdot BC-BC^2=0$. Dividiendo entre $AC^2$, llegamos a la ecuación de segundo grado
\[\left(\frac{BC}{AC}\right)^2+\frac{BC}{AC}-1=0\ \Longrightarrow\ \frac{BC}{AC}=\frac{-1\pm\sqrt{5}}{2}.\]
Tenemos que descartar la solución negativa, lo que nos dice finalmente que
\[BC=\frac{\sqrt{5}-1}{2}AC.\]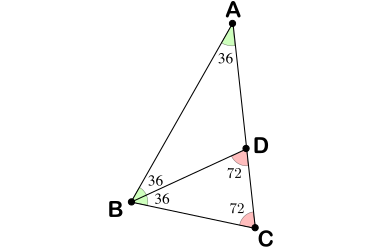
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre