Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 75
OIM, 1993-P4
Sea $ABC$ un triángulo equilátero y sean $M$ y $N$ puntos de $AB$ y $AC$, respectivamente, tales que el segmento $MN$ es tangente a la circunferencia inscrita de $ABC$. Demostrar que
\[\frac{AM}{MB}+\frac{AN}{NC}=1.\]
pistasolución 1info
Pista. Demostrar que el triángulo $AMN$ tiene perímetro igual al lado del triángulo equilátero inicial y, de ahí, sustituir $MB=MN+AN$ y $NC=MN+AM$.
Solución. Llamemos $T$ al punto de tangencia de $MN$ con la circunferencia inscrita y $\ell$ al lado del triángulo. Observemos que la longitud de $MT$ es igual a la del segmento que une $M$ con el punto medio del lado $AB$ por la propiedad de tangencia. Por tanto, $AM+MT=\frac{\ell}{2}$ y, de la misma forma, $AN+NT=\frac{\ell}{2}$, con lo que el perímetro del triángulo $AMN$ es exactamente $\ell$. Así, podemos escribir
\[\frac{AM}{MB}+\frac{AN}{NC}=\frac{AM}{MN+AN}+\frac{AN}{MN+AM}=\frac{AM^2+AN^2+MN(AN+AM)}{MN^2+MN(AN+AM)+AM\cdot AN}.\]
Por lo tanto, quisiéramos demostrar que $AM^2+AN^2=MN^2+AM\cdot AN$, pero esto se deduce de forma fácil del teorema del coseno aplicado al triángulo $AMN$ teniendo en cuenta que $\angle MAN=60^\circ$.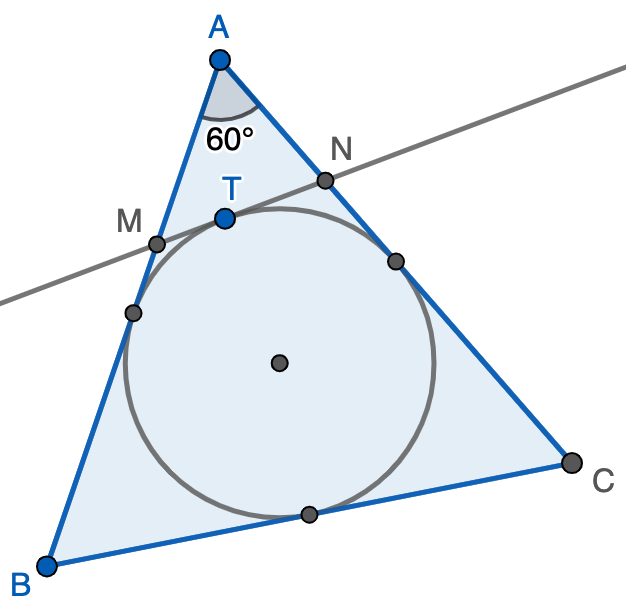

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre