Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 768
OIM, 2003-P5
En el cuadrado $ABCD$, sean $P$ y $Q$ puntos pertenecientes a los lados $BC$ y $CD$, respectivamente, distintos de los extremos y tales que $BP=CQ$. Se consideran puntos $X$ e $Y$, $X\neq Y$, pertenecientes a los segmentos $AP$ y $AQ$, respectivamente. Demuestre que, cualesquiera que sean $X$ e $Y$, existe un triángulo cuyos lados tienen las longitudes de $BX$, $XY$ y $DY$.
pistasolución 1info
Pista. Dobla el papel en el que has dibujado el cuadrado.
Solución. Si recortamos el cuadrado y también el triángulo $CPQ$, podemos doblar por las líneas $AP$ y $AQ$ para formar una pirámide con vértice en $A$. Observemos que, de esta forma $B$ se identifica con $D$ ya que ambos puntos están a la misma distancia de $A$. No obstante, para comprobar que efectivamente la pirámide se cierra, observamos que el triángulo de vértices $B=D$, $P$ y $Q$ en el espacio es rectángulo ya que es congruente con el triángulo $CPQ$ que hemos quitado. Ahora la solución al problema es evidente ya que $BX$, $XY$ y $DY$ forman un triángulo en el espacio.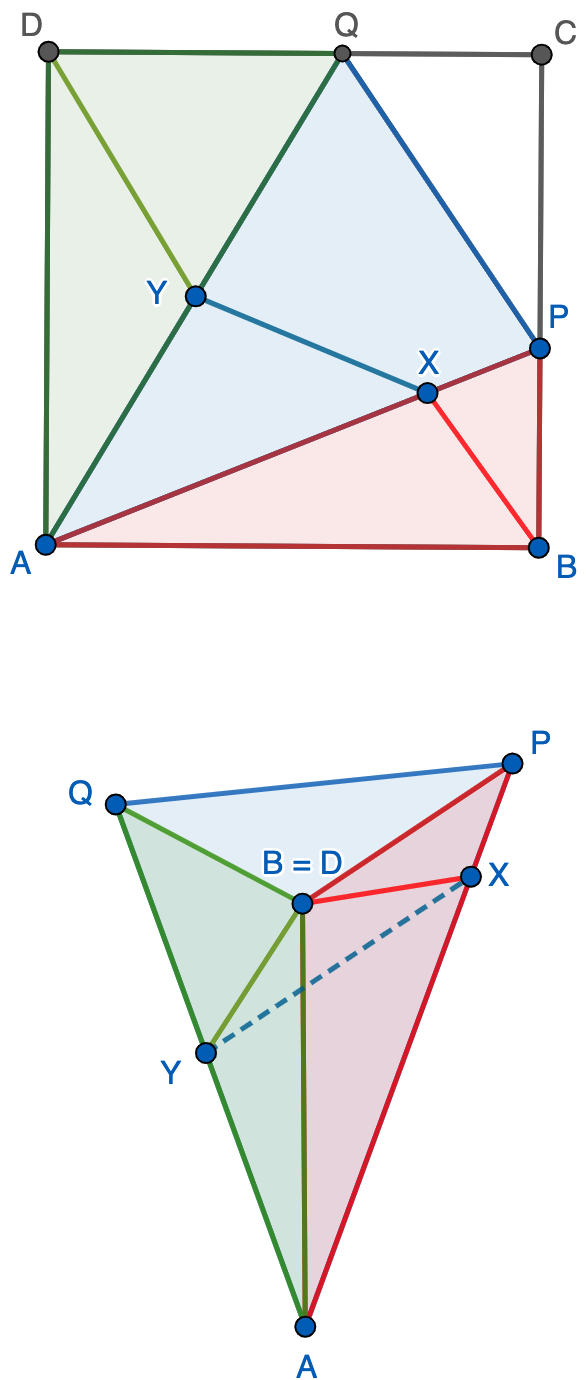

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre