Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 773
En el triángulo $ABC$ se traza la bisectriz interior $CD$. Se sabe que el centro del círculo inscrito en el triángulo $BCD$ coincide con el centro del círculo circunscrito del triángulo $ABC$. Calcular los ángulos del triángulo $ABC$.
pistasolución 1info
Pista. Calcula los ángulos del triángulo $OBC$, siendo $O$ el circuncentro de $ABC$.
Solución. Consideramos el circuncentro $O$ y el triángulo $OBC$, que está sombreado en la figura. Por un lado, tenemos que $\angle BCD=\frac{C}{2}$, por ser $BD$ la bisectriz, luego $\angle OCB=\frac{C}{4}$ ya que $OC$ es bisectriz del triángulo $BCD$. Por otro lado, tenemos que $\angle OBC=\frac{B}{2}$ ya que $OB$ es bisectriz de $BCD$. Finalmente, tenemos que $\angle BOC=2A$ ya que se trata del ángulo central del ángulo $A$ en el triángulo $ABC$.
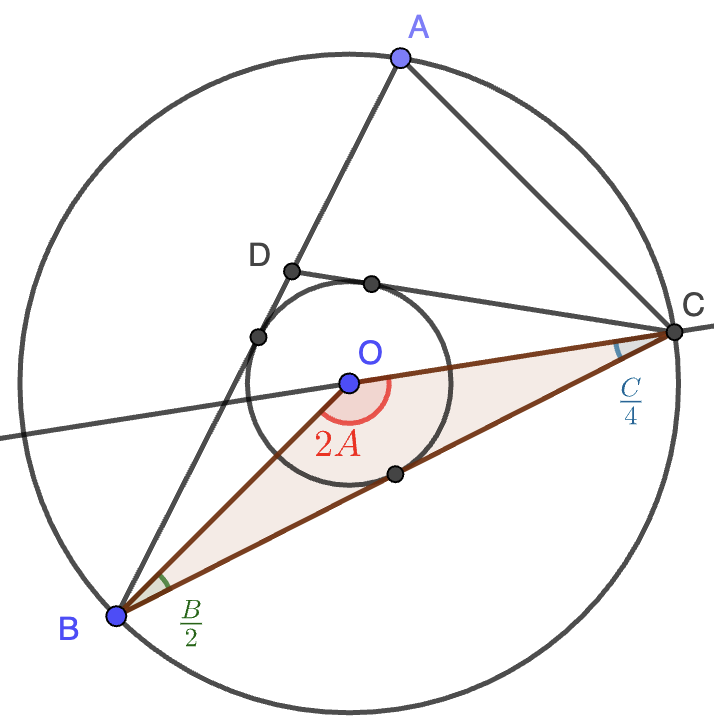
Tenemos así que $OBC$ tiene ángulos $2A$, $\frac{B}{2}$ y $\frac{C}{4}$. Este triángulo es isósceles dado que $OB=OC$ (son el radio de la circunferencia circunscrita), luego $\frac{C}{4}=\frac{B}{2}$. Nos quedan por tanto, tres ecuaciones sobre las incógnitas $A,B,C$, que forman el sistema lineal: \[\left\{\begin{array}{c} A+B+C=180\\ 2A+\frac{B}{2}+\frac{C}{4}=180\\ \frac{C}{4}=\frac{B}{2} \end{array}\right.\] Se resuelve fácilmente, dando solución única $A=C=72^\circ$ y $B=36^\circ$.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre