Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 784
Un poliedro convexo tiene por caras $12$ cuadrados, $8$ hexágonos regulares y $6$ octógonos regulares. En cada vértice del poliedro concurren exactamente un cuadrado, un hexágono y un octógono. ¿Cuántos segmentos que unen pares de vértices del poliedro son interiores al mismo, es decir, no son aristas ni están contenidos en una cara?
pistasolución 1info
Pista. ¿Cuántos vértices tiene el poliedro? ¿Cuántos vértices están en la misma cara que un vértice dado?
Solución. Si sumamos el número de cuadrados multiplicado por $4$, el número de hexágonos multiplicado por $6$ y el de octógonos multiplicado por $8$ obtendremos $3V$, siendo $V$ el número total de vértices. Por lo tanto,
\[V=\frac{12\cdot 4+6\cdot 8+8\cdot 6}{3}=48.\]
Ahora bien, de cada vértice salen tres aristas, una diagonal de un cuadrado, tres diagonales de un hexágono y 5 diagonales de un octógono, por lo que este vértice estará unido a otros $48-1-3-5=40$ vértices por segmentos interiores. Esto nos da un total de $40\cdot 48$ de tales segmentos, pero cada uno lo estamos contando dos veces (una por cada uno de sus extremos). Por tanto, el número de segmentos que buscamos es $\frac{1}{2}\cdot 40\cdot 48=960$.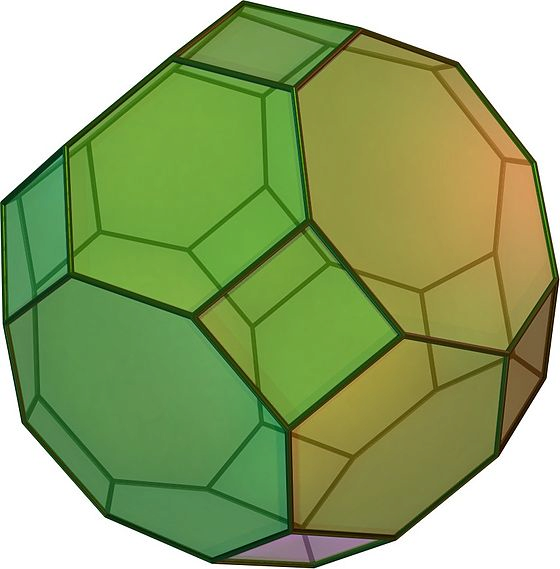

Nota. El poliedro en cuestión existe y se llama cuboctaedro truncado. Puede verse en la figura de arriba (extraída de Wikipedia). ¿Sabrías contar el número de aristas? ¿Sabrías probar que es el único poliedro tal que en cada vértice concurren un cuadrado, un hexágono y un octógono? En otras palabras, los datos de 12 cuadrados, 8 hexágonos y 6 octógonos son redundantes.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre