Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Consideremos los seis triángulos en que la figura queda dividida por las cevianas $AF$, $BD$ y $CE$ y llamemos a sus áreas $S_1,\ldots,S_6$ tal y como se indica en la figura. Vamos a obtener relaciones entre estas áreas usando que las áreas de dos triángulos que tienen la misma altura son proporcionales a las bases.

• El triángulo $APC$ tiene el triple del área de $AEP$ ya que tienen el altura común en $A$ y las bases son $9$ y $3$, respectivamente. Esto nos dice que $S_1+S_2=3S_6$.
• Los triángulos $BPC$ y $EPB$ están en la misma situación, lo que nos dice que $S_3+S_4=3S_5$.
• Los triángulos $APB$ y $APD$ tienen el mismo área ya que tienen iguales la base y la altura desde el vértice común $A$. Deducimos así que $S_5+S_6=S_1$.
• Los triángulos $EPB$ y $CPD$ tienen un ángulo igual (opuesto por el vértice $P$), luego rotando uo de ellos $180^\circ$ respecto de $P$, como $BP=PD$, deducimos que $S_2=3S_3$ (también puede usarse que el área es $\frac{1}{2}$ del producto de dos lados por el seno del ángulo que forman).

Con todo esto, tenemos tres ecuaciones lineales que involucran a las incógnitas $S_1$, $S_2$, $S_5$, $S_6$ y $S_3+S_4$. El sistema no es compatible determinado pero nos permite despejar en términos de $S_1$ el resto de áreas (¡compruébalo!): \[S_2=S_1,\qquad S_6=\frac{2}{3}S_2,\qquad S_5=\frac{1}{3}S_1,\qquad S_3+S_4=S_1.\] Ahora bien, si llamamos $x=AP$ y $20-x=PF$, podemos hacer un truco similar a los anteriores ya que las áreas de $APC$ y $PFC$ son proporcionales a $x$ y $20-x$ y también lo son las de $APB$ y $PBF$. Esto nos da las relaciones siguientes: \[\frac{S_1+S_2}{x}=\frac{S_3}{20-x},\qquad \frac{S_5+S_6}{x}=\frac{S_4}{20-x}.\] Sumando ambas expresiones y poniendo todo en función de $S_1$, nos queda \[\frac{S_1+S_2+S_5+S_6}{x}=\frac{S_4+S_5}{20-x}\ \Longleftrightarrow\ \frac{3S_1}{x}=\frac{S_1}{20-x}.\] Eliminando $S_1$ de ambos miembros, la ecuación se resuelve fácilmente y nos da $x=15$. Por lo tanto, también podemos despejar $S_3$ y $S_4$ en términos de $S_1$: \[S_3=\frac{20-x}{x}(S_1+S_2)=\frac{2}{3}S_1,\qquad S_4=\frac{20-x}{x}(S_5+S_6)=\frac{1}{3}S_1.\]

Ya solamente nos queda calcular $S_1$ y esta es la parte difícil. Como $S_1=S_2$, se sigue que $D$ es el punto medio de $AC$, luego $PD$ es la mediana de $APC$. La mediana puede calcularse en función de los lados como \[36=AD^2=\frac{AP^2+PC^2}{2}-\frac{AC^2}{4}=\frac{15^2+9^2}{2}-\frac{AC^2}{4}\ \Leftrightarrow\ AC^2=468,\] de donde $CD=\frac{1}{2}AC=\sqrt{117}$. Como $PC^2+PD^2=9^2+6^2=117$, el triángulo $DPC$ es rectángulo. y podemos calcular $S_1=S_2=\frac{1}{2}\cdot 6\cdot 9=27$. Por tanto, el área de $ABC$ es \[S_1+S_2+S_3+S_4+S_5+S_6=S_1+S_1+\frac{2}{3}S_1+\frac{1}{3}S_1+\frac{1}{3}S_1+\frac{2}{3}S_1=4S_1=108.\]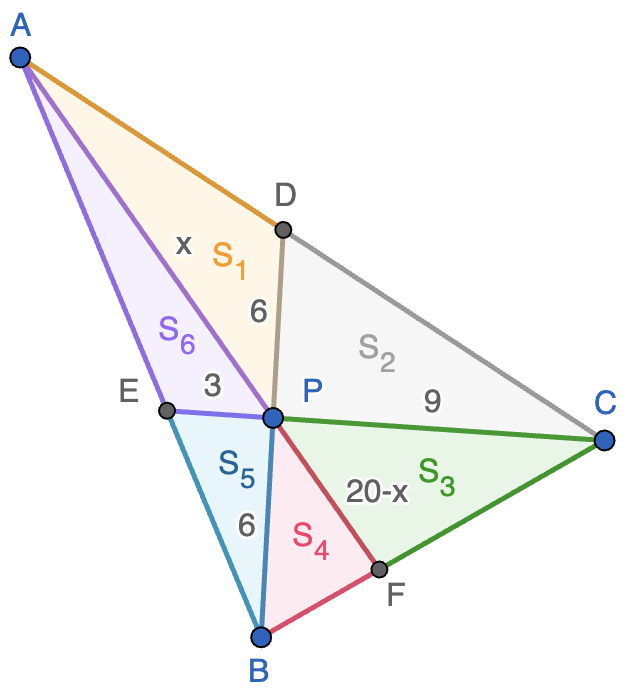

Nota. Si no nos damos cuenta en el paso final de que el triángulo es rectángulo, siempre podríamos haber usado la fórmula de Herón en $APD$. Es relativamente difícil caer en la cuenta de que $DPC$ es rectángulo (al escribir esta solución, se vio lo del triángulo rectángulo por haberlo dibujado previamente con Geogebra).