Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2748 problemas y 1042 soluciones.
Problema 787
Demostrar que en un triángulo la distancia de un vértice cualquiera al ortocentro es el doble de la distancia del circuncentro al lado opuesto a ese vértice.
pistasolución 1info
Pista. Hay muchas formas de demostrar este resultado. Considera el triángulo que se forma entre el circuncentro, el punto medio del lado y un vértice de ese lado. Este triángulo lo puedes duplicar haciendo homotecia de razón $2$ respecto de ese vértice.
Solución. Consideremos un triángulo $ABC$, su circuncentro $O$ y su ortocentro $H$. Si llamamos $M$ al punto medio del lado $BC$, tendremos que demostrar que $AH=2BC$. Para ello, trazamos el diámetro de la circunferencia circunscrita que pasa por $B$ y su punto diametralmente opuesto, que llamaremos $P$, como se indica en la figura. Por ser $BP$ un diámetro, se tiene que $PC$ es perpendicular a $BC$ y, por tanto, paralela a la mediatriz $OM$. Entonces, los triángulos $BOM$ y $BPC$ son semejantes y se cumple que $PC=2OM$, luego tendremos que demostrar que $PC=AH$. Esto último se sigue de que $APCH$ es un paralelogramo ya que $PC$ es paralela a la altura $AH$ y $AP$ es paralela a la altrua $CH$ (ya que el ángulo $\angle BAP$ es recto por comprender al diámetro $BP$).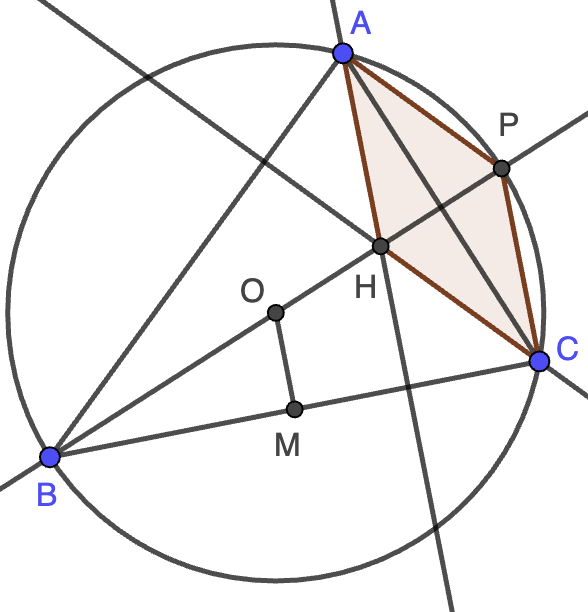

Nota. Este es un resultado relativamente conocido en el ámbito de la geometría de olimpiadas. ¿Sabrías probar que $AH=2R\cos A$ y $OM=R\cos A$, siendo $R$ el radio de la circunferencia circunscrita? ¿Sabrías probar a partir de este resultado que las rectas $OA$ y $MH$ se cortan en un punto de la circunferencia circunscrita?
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2025. Esta página ha sido creada mediante software libre