Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 794
OME Local, 2007-P12
Sea $P$ un punto interior a un triángulo $ABC$. Por $P$ se trazan paralelas $KP$, $MP$ y $NP$ a los lados $AB$, $AC$ y $BC$, respectivamente, que dividen el triángulo inicial en tres triángulos y tres paralelogramos. Sean $S_1$, $S_2$, $S_3$ las áreas de los nuevos triángulos y $S$ el área del triángulo $ABC$. Probar que
\[S\leq 3(S_1+S_2+S_3).\]
pistasolución 1info
Pista. Demuestra que las altura de $ABC$ es la suma de las alturas de los tres triángulos.
Solución. En la figura pueden verse los tres triángulos que tienen su vértice en $P$ dibujados de colores distintos. Trasladamos dos de ellos de forma paralela a los lados hasta que se apoyen los tres sobre un mismo lado del triángulo (en la figura hemos elegido el lado $AB$). Los tres triángulos así obtenidos son semejantes pues tienen sus lados paralelos a los lados del triángulo original. Por tanto, sus áreas serán proporcionales al cuadrado de sus alturas, es decir, $S_1=\lambda h_1^2$, $S_2=\lambda h_2^2$, $S_3=\lambda h_3^2$ para cierta constante positiva $\lambda$. Por otro lado, la altura del triángulo grande $ABC$ es $h_1+h_2+h_3$ y también es semejante a los tres triángulos pequeños, luego $S=\lambda(h_1+h_2+h_3)^2$ y la desigualdad a probar se puede reescribir como
\[(h_1+h_2+h_3)^2\leq 3(h_1^2+h_2^2+h_3^2)\]
ya que podemos cancelar $\lambda$ en ambos miembros. Desarrollando el cuadrado y agrupando términos, esta desigualdad se puede reescribir como
\[0\leq 2(h_1^2+h_2^2+h_3^2-h_1h_2-h_1h_3-h_2h_3)=(h_1-h_2)^2+(h_2-h_3)^2+(h_3-h_1)^2,\]
que es obviamente cierta.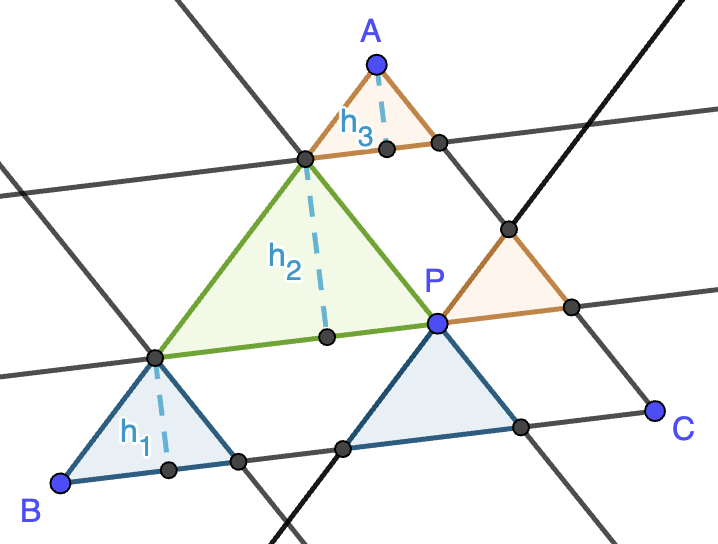

Nota. La igualdad se cumple cuando $h_1=h_2=h_3$, luego los tres triángulos pequeños deben ser iguales (congruentes). Esto se cumple si y solo si $P$ es el baricentro del triángulo. ¿Sabrías demostrarlo?
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre