Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 799
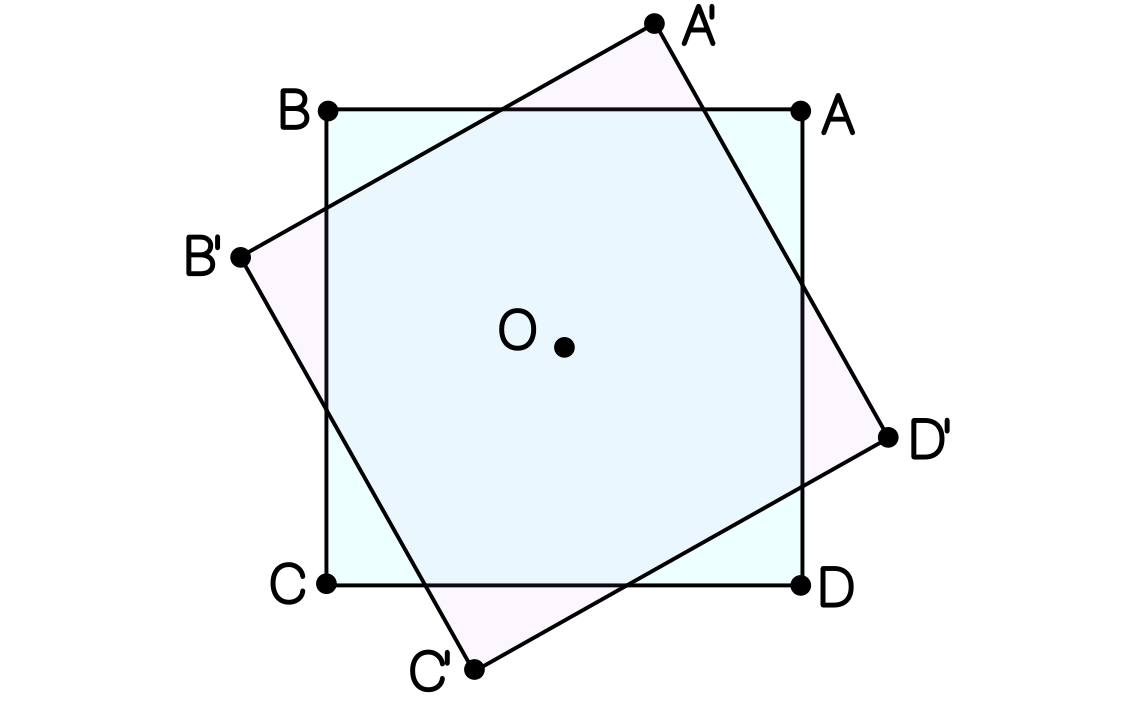
Un cuadrado $ABCD$ de lado $1$ gira un ángulo $\alpha$ en torno a su centro $O$. Hallar el área común a ambos cuadrados.
pistasolución 1info
Pista. El octógono se descompone en $8$ triángulos congruentes de altura $\frac{1}{2}$. Calcula la base correspondiente en términos de $\alpha$.
Solución. Consideremos los puntos $P$ y $Q$ indicados en la figura de abajo. Por simetría, el área se descompone en $8$ triángulos congruentes a $OPQ$. Este último triángulo, sombreado en la figura, tiene base $PQ$ y altura $\frac{1}{2}$, luego el área que nos piden es $S=8\cdot\frac{1}{2}\cdot\frac{1}{2}\cdot PQ=2 PQ$ y será suficiente calcular la longitud de $PQ$ en función de $\alpha=\angle A'PQ$.
Por la simetría de la figura y usando trigonometría en el triángulo $A'PQ$, obtenemos que $BP=A'P=PQ\cos\alpha$. Análogamente, tenemos que $AQ=A'Q=PQ\operatorname{sen}\alpha$, con lo que
\[1=AB=AQ+PQ+BP=PQ(1+\operatorname{sen}\alpha+\cos\alpha).\]
Esto nos lleva a la solución del problema
\[S=2PQ=\frac{2}{1+\operatorname{sen}\alpha+\cos\alpha}.\]
Nota. La solución presupone que $\alpha\in[0,90]$ implícitamente. Para un valor de $\alpha$ general, por la simetría de la construcción basta reducirlo módulo $90$ a un ángulo de dicho intervalo.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre