Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 801
Determina los valores de $n$ para los que es posible construir un cuadrado $n\times n$ ensamblando tetrominós como el de la figura (formado por cuatro cuadraditos $1\times 1$).

pistasolución 1info
Pista. Colorea el cuadrado como un tablero de ajedrez.
Solución. Lo primero que observamos es que si $n$ es impar, entonces el tablero tiene un número impar de casillas y no se puede rellenar con un número entero de fichas, cada una de las cuales ocupa cuatro casillas. Por tanto, supondremos que es par en lo que sigue. Distingamos dos casos:
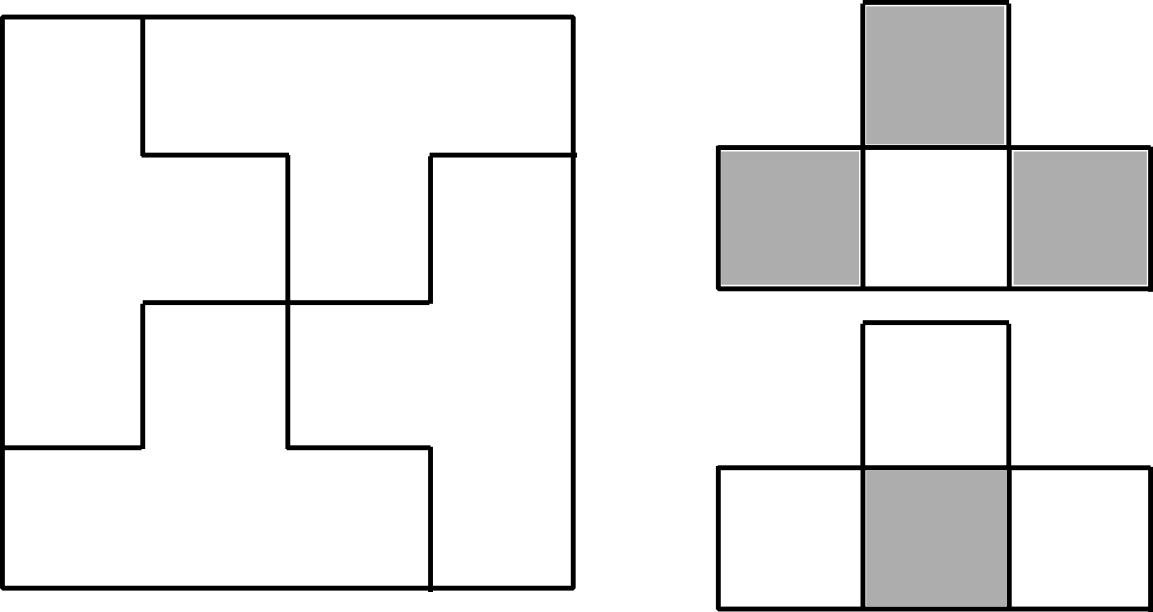
- Si $n=4k$, entonces el cuadrado se puede construir. Para ello, basta descomponerlo en cuadrados $4\times 4$ (mediante rectas paralelas a los lados del cuadrado y rellenar cada uno de ellos con cuatro tetrominós como se indica en la figura de la izquierda.
- Si $n=4k+2$, vamos a probar que el cuadrado no se puede construir. Para ello, coloreamos el cuadrado como un tablero de ajedrez, alternando colores blanco y negro en casillas adyacentes. Cada tetrominó ocupa o bien tres casillas blancas y una negra o bien tres negras y una blanca (como los que se indican en la figura de la derecha). Llamamos $a$ al número de tetrominós del primer tipo y $b$ al del segundo tipo en un supuesto ensamblado. Como hay el mismo número de casillas blancas que negras ($n$ es par), se sigue que $a+b$ es par, luego $n^2=4(a+b)$ es múltiplo de $8$. Esto no es posible si $n=4k+2$, luego el ensamblado es imposible.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre