Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Sean $X,Y,Z$ los pies de las perpendiculares desde $P$ a los lados $BC,AC,AB$, respectivamente. Vamos a demostrar que $XPY$ es semejante a $ZPX$, probando que dos de sus ángulos son iguales. Esta semejanza nos dirá que $\frac{ZP}{PX}=\frac{PX}{PY}$, que equivale a $a^2=bc$. Vamos a distinguir dos casos, suponiendo previamente que $P\neq B$ y $P\neq C$ (en tal caso la igualdad $a^2=bc$ es cierta ya que queda $0=0$).

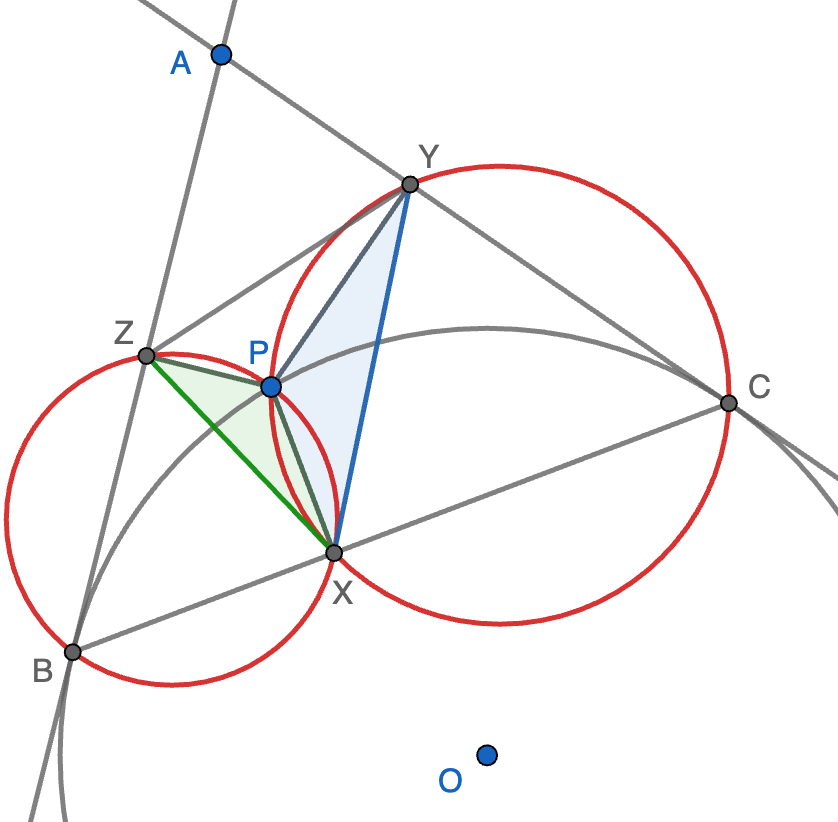
El primer caso es que $P$ sea interior al triángulo $ABC$. Los cuadriláteros $ZPBX$ e $YPXC$ son cíclicos ya que tienen dos ángulos rectos opuestos. La propiedad del arco capaz nos dice que $\angle XPY=180-\angle ACB$ y $\angle ZPX=180-\angle ABC$; como se tiene que $\angle ACB=\angle ABC$ por ser $ABC$ isósceles, se deduce que $\angle XPY=\angle ZPX$ y ya tenemos un ángulo igual. Para el segundo ángulo, calculamos de nuevo por arco capaz \begin{align*} \angle PXY-\angle ZPX&=\angle PCY-\angle PBX=\angle ACB-\angle PCX-\angle PBX\\ &=\angle ACB-180+\angle BPC. \end{align*} En el último paso hemos usado que los ángulos del triángulo $BPC$ suman $180$. Ahora bien, $\angle BOC=360-2\angle BPC$ por la propiedad del arco central, donde $O$ es el centro de la circunferencia tangente a los lados. Como en el cuadrilátero $ABCO$ los ángulos suman $360$ y dos de ellos son rectos, llegamos a que $\angle BOC=180-\angle BAC$ y, por tanto, $\angle BPC=90+\frac{1}{2}\angle BAC=180-\angle ACB$ (ya que $ABC$ es isósceles). Volviendo al cálculo anterior, tenemos que $\angle PXY-\angle ZPX=0$, lo que concluye la demostración de que $XPY$ es semejante a $ZPX$.

El segundo caso es que $P$ sea exterior al triángulo $ABC$, es decir, $P$ está en el arco mayor $BC$ de la circunferencia. La demostración se adapta pero los cálculos son ligeramente distintos. La igualdad $\angle XPY=\angle ZPX$ es cierta pero en este caso porque los dos ángulos son iguales a $180-\angle ABC$. Para la otra igualdad de ángulo, calculamos \begin{align*} \angle PXY-\angle ZPX&=\angle PCY-\angle PBX=180-\angle ACB-\angle PCX-\angle PBX\\ &=\angle ACB+\angle BPC=\angle ACB+\tfrac{1}{2}\angle BOC=\angle ACB+\tfrac{1}{2}(180-\angle BAC)=0. \end{align*}