Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
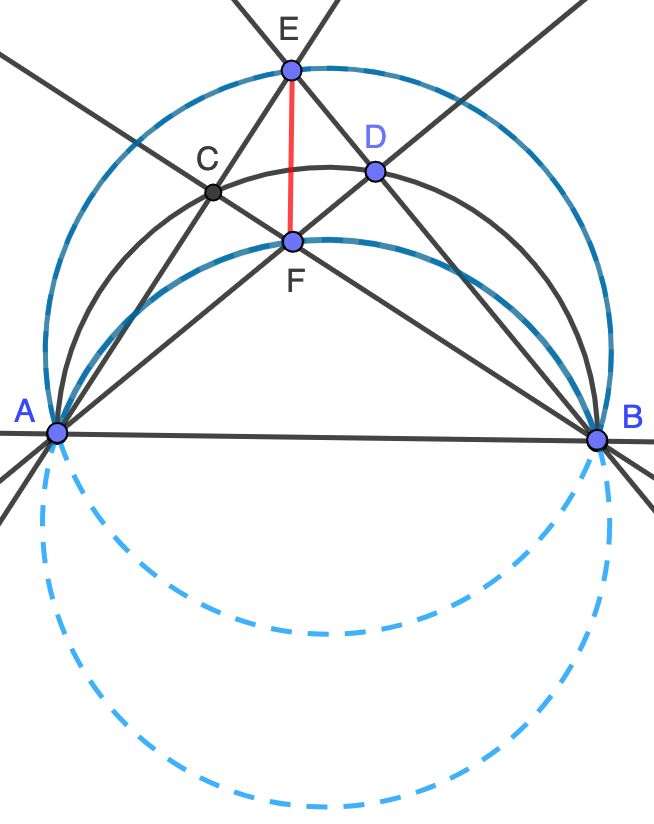
Es muy fácil darse cuenta de la recta $EF$ ha de ser perpendicular a $AB$: dado que los ángulos $\angle ACB$ y $\angle ADB$ son rectos por comprender al diámetro $AB$ en la semicircunferencia, se tiene que $AD$ y $BC$ son alturas del triángulo $AEB$, luego $F$ es su ortocentro y $EF$ es la tercera altura, que debe ser perpendicular al lado $AB$. Tenemos así que la dirección del segmento $EF$ no varía.
Veamos ahora que su longitud tampoco varía. Por la propiedad del arco capaz, el ángulo $\alpha=\angle CAD=\angle CBD$ sólo depende de $c$, no de la posición concreta de la cuerda $CD$. Como los ángulos $\angle ACB$ y $\angle ADB$ son rectos por comprender al diámetro $AB$ en la semicircunferencia, deducimos que $\angle AEB=90-\alpha$. Además, como la suma de los ángulos del cuadrilátero $ECFD$ es $360$, tenemos también que $\angle AFB=\angle CFD=90+\alpha$. Todo ello nos dice que los puntos $E$ y $F$ se mueven en sendos arcos de circunferencia con extremos $A$ y $B$ (al variar la cuerda $CD$ sin modificar su longitud), como puede verse en la figura. Además, como los ángulos con los que $E$ y $F$ ven al segmento $AB$ son $90-\alpha$ y $90+\alpha$, que suman $180$, estas circunferencias son simétricas respecto de $AB$. En particular, tienen el mismo radio y, al pasar por $A$ y $B$, tiene que ser una trasladada de la otra en la dirección perpendicular a $AB$. De esta forma, la longitud del segmento $EF$ es la del vector de traslación, o sea, constante.
Informar de error en enunciado Informar de procedencia del problema