Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Llamamos $ABCD$ al cuadrilátero y $P$ al punto de intersección de sus diagonales. Supondremos que las diagonales no son perpendiculares para que las proyecciones $A',B',C',D'$ definan un cuadrilátero, luego además se cumple que $P$ se queda entre $A'$ y $C'$ en la diagonal $AC$ y también entre $B'$ y $D'$ en la diagonal $BD$. Esto demuestra que el cuadrilátero $A'B'C'D'$ es convexo y tiene las mismas rectas diagonales que $ABCD$.

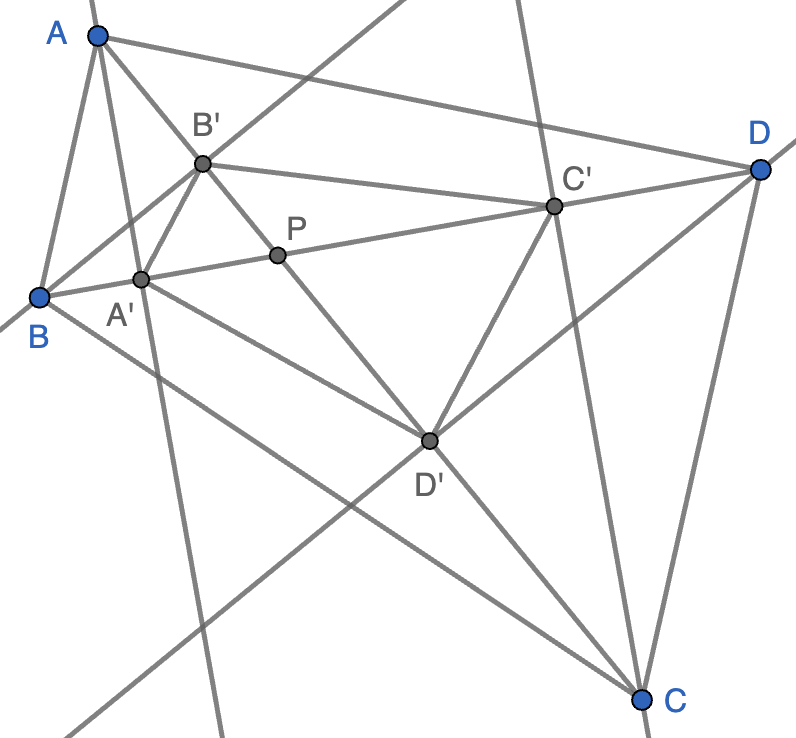
Los triángulos $AA'P$ y $BB'P$ son semejantes porque son rectángulos y tienen un ángulo común en el vértice $P$, luego se cumple que \[\frac{AP}{BP}=\frac{A'P}{B'P},\] lo que también nos dice que $ABP$ y $A'B'P$ son semejantes. De forma similar se prueba que $BCP$ y $B'C'P$ son semejantes, que $CDP$ y $C'D'P$ son semejantes y que $DAP$ y $D'A'P$ son semejantes. La razón de semejanza es la misma para los cuatro pares de triángulos ya que se tiene que $\frac{AP}{A'P}=\frac{BP}{B'P}=\frac{CP}{C'P}=\frac{DP}{D'P}$, luego el cuadrilátero $A'B'C'D'$ es semejante a $ABCD$ ya que está formado por cuatro triángulos semejantes en disposición similar. Más aún, $A'B'C'D'$ se obtiene de $ABCD$ a partir de una reflexión respecto de una de las bisectrices de las diagonales y una homotecia.