Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 831
Dada una circunferencia y dos puntos $P$ y $Q$ en su interior, inscribir un triángulo rectángulo cuyos catetos pasen por $P$ y $Q$. ¿Para qué posiciones de $P$ y $Q$ el problema no tiene solución?
pistasolución 1info
Pista. Al inscribir un triángulo rectángulo, la hipotenusa debe ser un diámetro.
Solución. Sea $\Gamma$ la circunferencia que nos dan, con centro $O$ y radio $R$. El problema es equivalente a encontrar un punto $X\in\Gamma$ tal que $PQX$ sea un triángulo rectángulo con ángulo recto en $X$ pues que en tal caso bastaría prolongar los lados $PX$ y $QX$ hasta que corten en sendos puntos $Y$ y $Z$ a la circunferencia (distintos de $X$), de forma que $XYZ$ es el triángulo inscrito que buscamos. El lugar geométrico de los puntos $X$ tales que $PQX$ es rectángulo con ángulo recto en $X$ es la circunferencia de diámetro $PQ$, luego existirá el punto que buscamos si y solo si la circunferencia de diámetro $PQ$ corta a $\Gamma$ Como la circunferencia de diámetro $PQ$ tiene centro en $M$, el punto medio de $PQ$, el problema tiene solución si y solo si $OM+MP\geq R$ (observemos que $OM+MP$ es la distancia más alejada de $O$ que se puede alcanzar con la circunferencia de diámetro $PQ$).
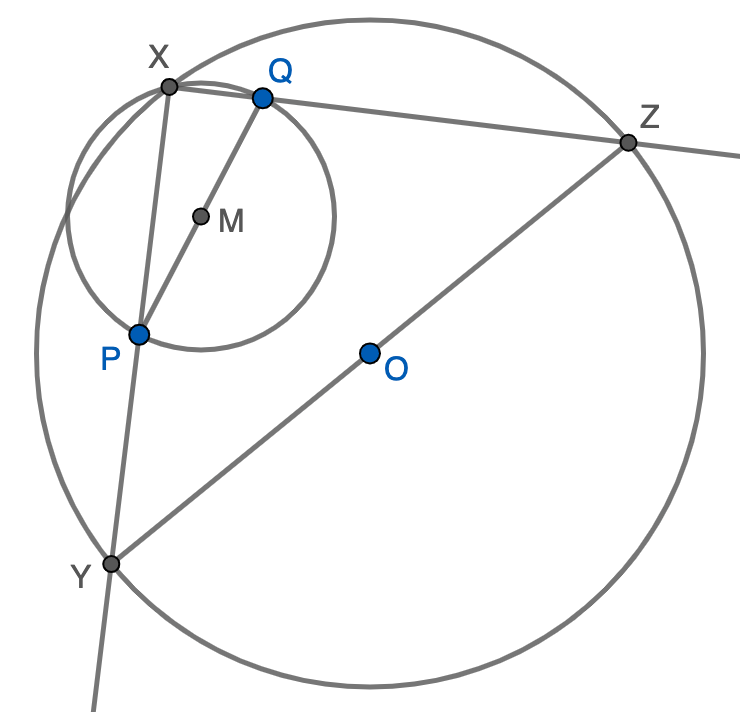
Para terminar, vamos a expresar el resultado sin que intervenga $M$, por rizar el rizo. Tenemos que $MP=\frac{1}{2}PQ$ y que $OM$ es la mediana de $OPQ$. Usando la fórmula de la meidana, la condición que buscamos se puede escribir finalmente como \[\frac{1}{2}PQ+\sqrt{\frac{OP^2+OQ^2}{2}-\frac{PQ^2}{4}}\geq R.\]

Nota. En realidad, cuando la desigualdad es estricta, hay dos soluciones ya que hay dos puntos de corte de ambas circunferencias.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre