Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 836
OME Local, 2008-P10
Determina el triángulo de menor perímetro de entre todos los que tienen la
circunferencia inscrita con el mismo radio y el mismo valor de un ángulo.
pistasolución 1info
Pista. El problema equivale a encontrar el triángulo de menor área. Demuestra que la solución es el triángulo isósceles con ese ángulo como ángulo desigual y ese radio inscrito viendo que otro triángulo en las mismas condiciones tiene necesariamente mayor área.
Solución. Sea $ABC$ el triángulo en cuestión y supongamos que el ángulo en $A$ está fijo y también el radio $r$ de la circunferencia inscrita, que es tangente a los lados en los puntos $X,Y,Z$, como se muestra en la figura. El área del triángulo está dada por $S=rp$, siendo $p$ el semiperímetro, luego minimizar el perímetro del triángulo equivale a minimizar su área cuando variamos $X$ en el arco mayor $YZ$. Es fácil intuir que la solución al problema es el triángulo isósceles $ARS$ tangente a la circunferencia inscrita en el punto medio $M$ de $RS$. Vamos a confirmar esta intuición viendo que cualquier otra elección de $X$ distinta de $M$ nos da un triángulo $ABC$ de área mayor que $ARS$. Si suponemos sin perder generalidad que $X$ está en el arco $MZ$ (en caso de estar en $MY$ el razonamiento es similar), probaremos que el área de $PBR$ (en verde) es menor que el área de $PCS$ (en azul), siendo $P$ el punto en de corte entre $BC$ y $RS$.
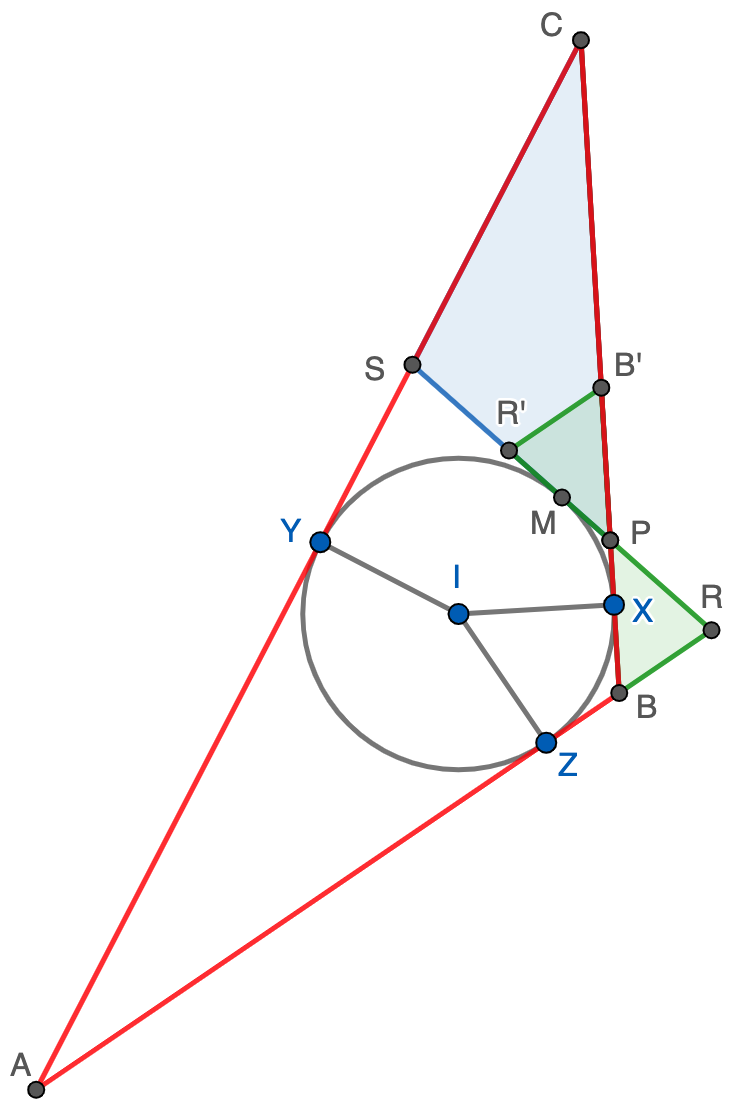
Como $P$ está en el segmento $MR$ y $M$ es el punto medio de $RS$, se sigue que $PR\lt PS$; además, se tiene que $\angle PRB$ es agudo mientras que $\angle CSR=180-\angle PRB$ es obtuso. Esto nos dice que si giramos $180^\circ$ el triángulo $PRB$ respecto de $P$ obtenemos un triángulo $PR'B'$ contenido en $PCS$, luego ciertamente el área de $PBR$ es menor que el área de $PCS$ y hemos terminado la demostración.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre