Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 849
OME Local, 2009-P12
Sean $C_1$ y $C_2$ dos circunferencias exteriores tangentes en el punto $P$. Por un punto $A$ de $C_2$ trazamos dos rectas tangentes a $C_1$ en los puntos $M$ y $M'$. Sean $N$ y $N'$ los puntos respectivos de corte, distintos ambos de $A$, de estas rectas con $C_2$. Probar que $PN'\cdot MN=PN\cdot M'N'$.
pistasolución 1info
Pista. Usa las potencias de $N$ y $N'$ respecto de $C_1$.
Solución. La rectas $PN$ y $PN'$ cortan de nuevo a $C_1$ en los puntos $R$ y $S$, respectivamente (estos puntos son distintos de $P$), como se muestra en la figura. Por la propiedad de la potencia de los puntos $N$ y $N'$ respecto de $C_1$ y usando las tangencias en $M$ y $M'$, obtenemos que
\[MN^2=PN\cdot RN,\qquad\text{y}\qquad (M'N')^2=PN'\cdot SN'.\]
Multiplicando la primera igualdad por $(PN')^2$ y la segunda por $PN^2$, llegamos a
\[MN^2\cdot (PN')^2=PN\cdot (PN')^2\cdot RN,\qquad\text{y}\qquad (M'N')^2\cdot PN^2=PN'\cdot PN^2\cdot SN',\]
a la vista de lo cual será suficiente ver que $PN'\cdot RN=PN\cdot SN'$, lo cual se deduce de la semejanza de los triángulos $PNN'$ y $PRS$ (se puede transformar uno en otro usando la homotecia de centro en $P$ que lleva $C_1$ en $C_2$, ¿sabrías justificarlo?). Concretamente, tenemos que
\[\frac{PN}{PN'}=\frac{PR}{PS}=\frac{PR+PN}{PS+PN'}=\frac{RN}{SN'}.\]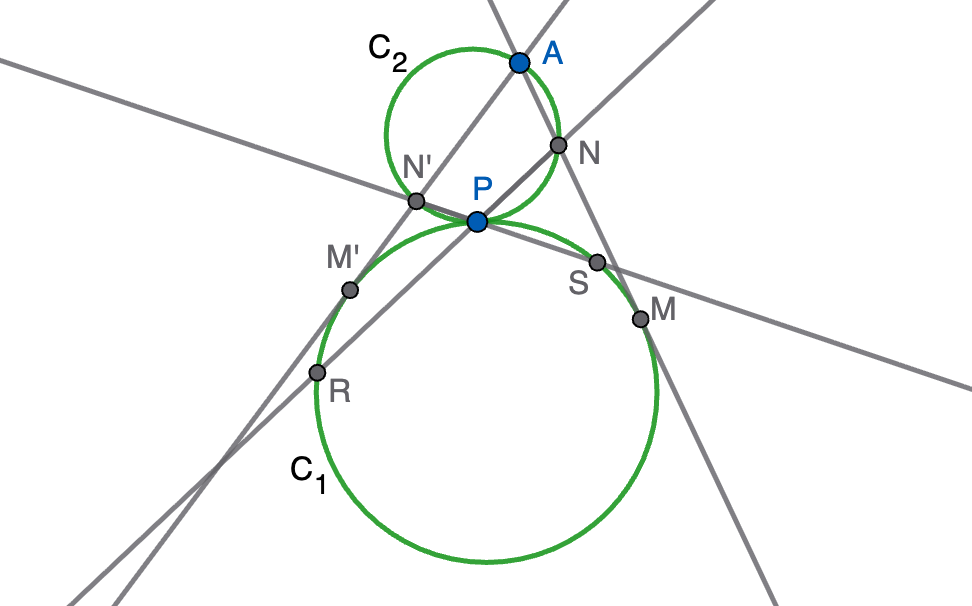

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre