Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 856
OIM, 2009-P1
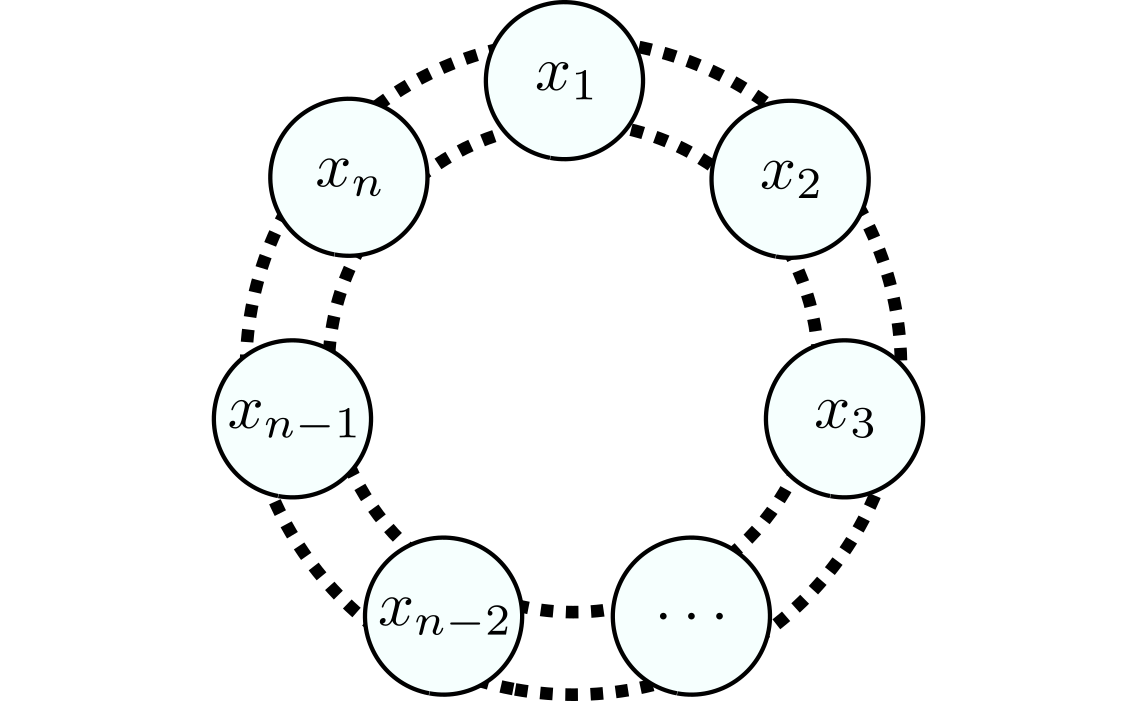
Sea $n\geq 3$ un entero. Supongamos que $n$ islas están ubicadas en un círculo y que entre cada dos islas vecinas hay dos puentes como en la figura.
Comenzando en la isla $x_1$, ¿de cuántas maneras se pueden recorrer los $2n$ puentes pasando por cada puente exactamente una vez?
pistasolución 1info
Pista. Se puede recorrer los puentes dándose la vuelta en algún $x_k$ o bien siempre girando en el mismo sentido. Halla por separado cuántas formas hay de hacer cada uno de esos recorridos. Ten en cuenta que puedes empezar girando en sentido horario o antihorario. Lo difícil de este problema es no dejarse ningún caso.
Solución. Una observación inicial importante que ayuda a centrar el problema, es que siempre se acaba en $x_1$. De esta manera, está claro que hay dos maneras esencialmente distintas de hacer el recorrido:
- Empezando en $x_1$, llegar hasta un cierto $x_k$, darnos la vuelta hasta regresar a $x_1$ y luego volver hasta $x_k$ por el otro lado y terminar de nuevo en $x_1$. Para llegar hasta $x_k$ en sentido horario tenemos $2^{k-1}$ posibilidades (equivale a elegir en cada isla uno de los dos puentes a la ida ya que a la vuelta tendremos que volver por el que no hemos elegido a la ida) y $2^{n-k+1}$ posibilidades para ir de $x_1$ a $x_k$ en sentido horario. Esto da $2^{k-1}2^{n-k+1}=2^n$ posibles caminos. Como esto ocurre para cada $k$ y podemos ir primero en sentido horario o primero en sentido antihorario, el número total de posibles caminos en este caso es $2n\cdot 2^n=2^{n+1}n$.
- Empezando en $x_1$ no nos damos la vuelta en ningún sitio sino que vamos girando siempre en sentido horario o antihorario dando dos vueltas a todo el círculo. Tendremos también $2^n$ posibles caminos en cada sentido de giro (ya que solo hay que elegir puente en la primera vuelta). Esto nos da $2^{n+1}$ posibilidades.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre