Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 865
Se considera un triángulo equilátero de lado $1$ y centro $O$, como el de la figura. Un rayo parte de $O$ y se refleja tres veces: primero en el lado $AB$, después en el lado $AC$ y finalmente en el lado $BC$. El rayo termina alcanzando el vértice $A$. Determinar la longitud mínima de un rayo en tales condiciones.
Nota. Cuando un rayo se refleja en un lado, los ángulos de entrada (incidencia) y salida (reflexión) coinciden.

pistasolución 1info
Pista. Refleja el triángulo $ABC$ respecto de sus lados.
Solución. Si reflejamos repetidamente el triángulo respecto de sus lados, entonces la poligonal que forma la trayectoria del rayo se vuelve una línea recta ya que el ángulo de incidencia es el de reflexión. Como nos dicen que se refleja primero respecto de $AB$, luego $AC$ y por último $BC$, estas son las reflexiones que debemos hacer y que hemos dibujado en la figura. Vemos así que hay una única forma hacer los rebotes para que se cumpla la condición del enunciado y ahora solamente hay que calcular su longitud.
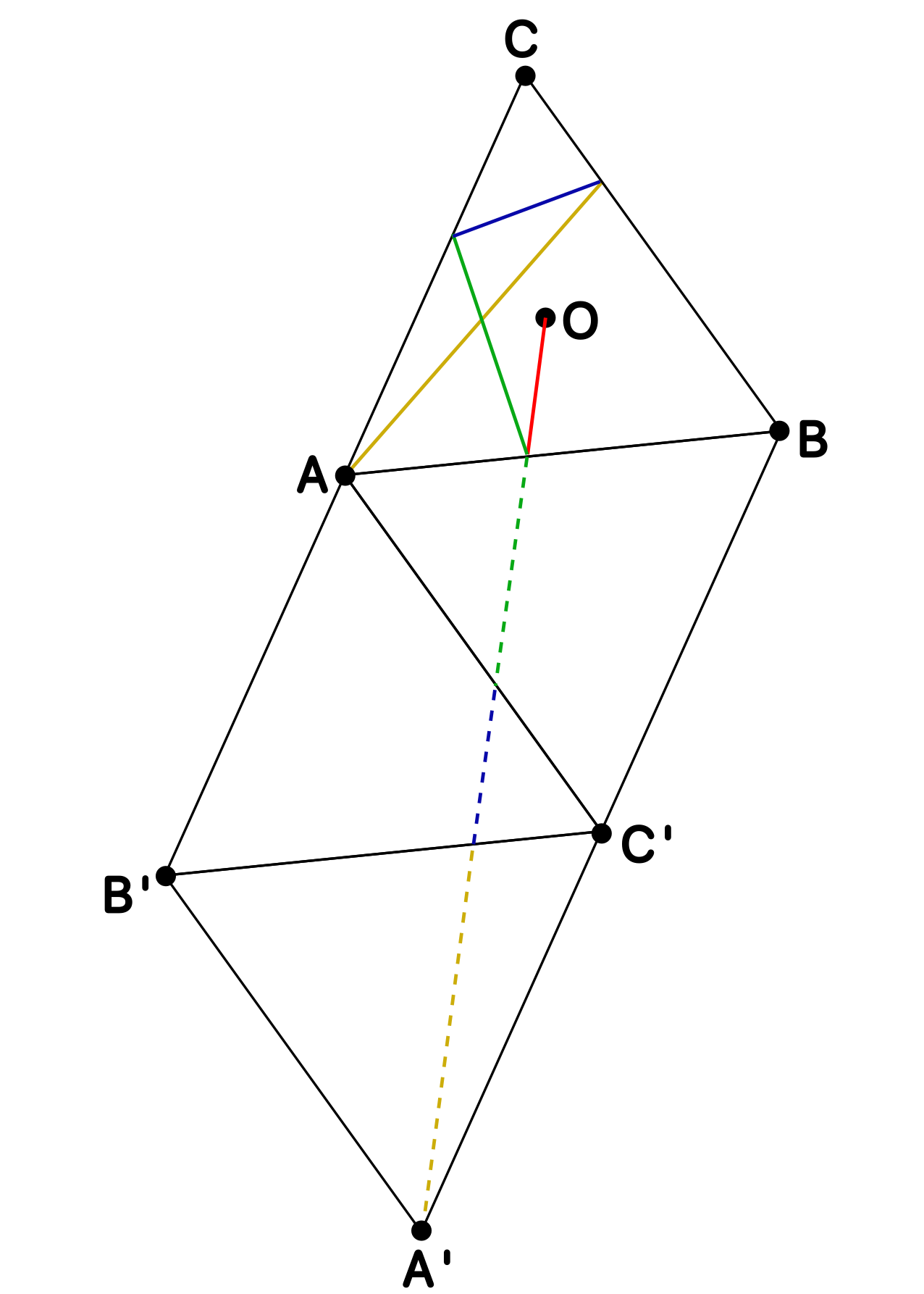
Para ello, observamos que $OBA'$ es un triángulo rectángulo ya que $OB$ es una altura del triángulo equilátero y $BA'$ es paralela al lado opuesto. Además, se tiene que $OB=\frac{2}{3}\cdot\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}$ (dos tercios de la altura) y $BA'=2$ (dos veces el lado), luego el teorema de Pitágoras nos da la distancia que buscamos: \[OA'=\sqrt{\left(\tfrac{\sqrt{3}}{3}\right)^2+2^2}=\frac{\sqrt{39}}{3}.\]

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre