Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 869
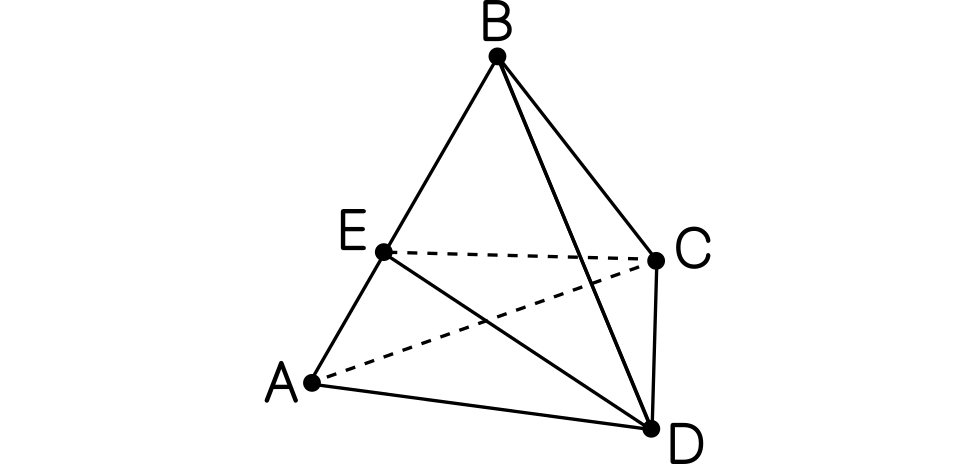
Se considera un tetraedro regular como el de la figura. Si el punto $E$ recorre la arista $AB$. ¿Cuándo el ángulo $\angle CED$ es máximo?
pistasolución 1info
Pista. Si $M$ es el punto medio de $CD$, demuestra el ángulo será máximo cuando la longitud de $EM$ sea mínima.
Solución. Sea $M$ el punto medio de $CD$, de forma que $EM$ es una altura del triángulo isósceles $CDE$. El ángulo $\alpha=\angle CED$ verifica que $\mathrm{tan}(\frac{\alpha}{2})=\frac{CM}{EM}$. El ángulo será máximo cuando la tangente sea máxima, es decir, cuando $EM$ sea mínimo ya que $CM$ no depende de dónde hayamos puesto el punto $E$. Ahora podemos restringirnos al plano que contiene al triángulo $ABM$. El segmento $EM$ está en este plano y su longitud será mínima cuando $EM$ sea perpendicular a $AB$, es decir, cuando $EM$ sea una altura de $ABM$, que coincide con la mediatriz por ser $ABM$ isósceles. Concluimos que el ángulo $\angle CED$ es máximo cuando $E$ es el punto medio de $AB$.
Nota. Usando el seno en lugar de la tangente, también puede razonarse de forma similar que lo que hay que minimizar es la longitud de $CE$, lo que nos lleva a que ha de ser perpendicular a $AC$ y $E$ tiene que ser el punto medio.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre