Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 886problema obsoleto
Dos semirrectas tienen su común origen en el punto $O$. Se considera una
circunferencia $C_1$ tangente a ambas semirrectas cuyo centro está situado
a distancia $d_1$ de $O$ y cuyo radio es $r_1$. Se construyen sucesivamente las circunferencias $C_n$, de modo que $C_n$ es tangente a las semirrectas, tangente exterior a $C_{n−1}$ y tal que la distancia de su centro a $O$, $d_n$, es menor que $d_{n−1}$ para $n\gt 1$. Halla la suma de las áreas de los círculos limitados por las circunferencias $C_n$ para todo $n$ en función de $r_1$ y $d_1$.
pistasolución 1info
Pista. Date cuenta de que existe una homotecia que lleva $C_k$ en $C_{k+1}$ para todo $k$. ¿Cuál es la razón de esta homotecia en términos de $r_1$ y $d_1$?
Solución. Sea $O_1$ el centro de $C_1$, que está sobre la bisectriz de las semirrectas dadas. Entonces, para pasar de la circunferencia $C_1$ a $C_2$, podemos hacer una homotecia de centro $O$ que lleva uno de los puntos de corte de $C_1$ con la bisectriz en el otro. Como el punto más alejado está a distancia $d_1+r_1$ y el más cercano a distancia $d_1-r_1$, la razón de la homotecia es $\lambda=\frac{d_1-r_1}{d_1+r_1}$. Como la homotecia transforma las áreas en un factor $\lambda^2$ y lleva cada circunferencia $C_k$ en $C_{k+1}$, tenemos que
\[\sum_{k=1}^n\mathrm{Area}(C_k)=\sum_{k=1}^n\lambda^{2k-2}\mathrm{Area}(C_1)=\frac{\pi r_1^2(1-\lambda^{2n+2})}{1-\lambda^2},\]
donde hemos usado la fórmula de la suma de los términos de una progresión geométrica. En el límite de esta suma cuando $n\to\infty$ el término $\lambda^{2n+2}$ tiene límite $0$ (ya que $0\lt \lambda\lt 1$) y el resultado es
\begin{align*}
\sum_{k=1}^\infty\mathrm{Area}(C_k)&=\frac{\pi r_1^2}{1-\lambda^2}=\frac{\pi r_1^2(d_1+r_1)^2}{(d_1+r_1)^2-(d_1-r_1)^2}\\
&=\frac{\pi r_1^2(d_1+r_1)^2}{4r_1d_1}=\frac{\pi r_1}{4d_1}(d_1+r_1)^2.
\end{align*}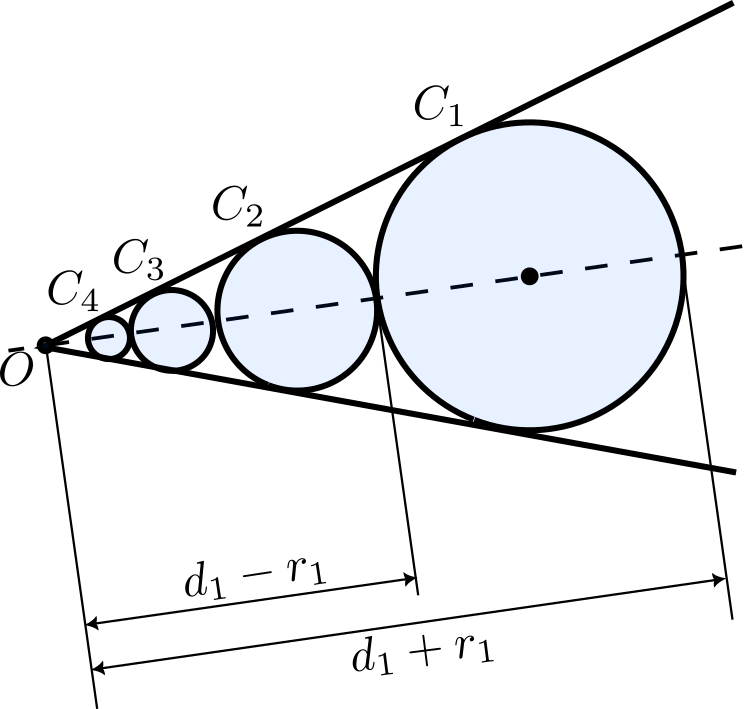

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre