Demuestra que en un triángulo se verifica: si $r$ es una recta que pasa por su baricentro y no pasa por ningún vértice, la suma de las distancias a dicha
recta de los vértices que quedan en un mismo semiplano es igual a la distancia del tercer vértice a dicha recta.
pistasolución 1solución 2info
Pista. Usa coordenadas y recuerda que las coordenadas del baricentro son la media aritmética de las coordenadas de los vértices.
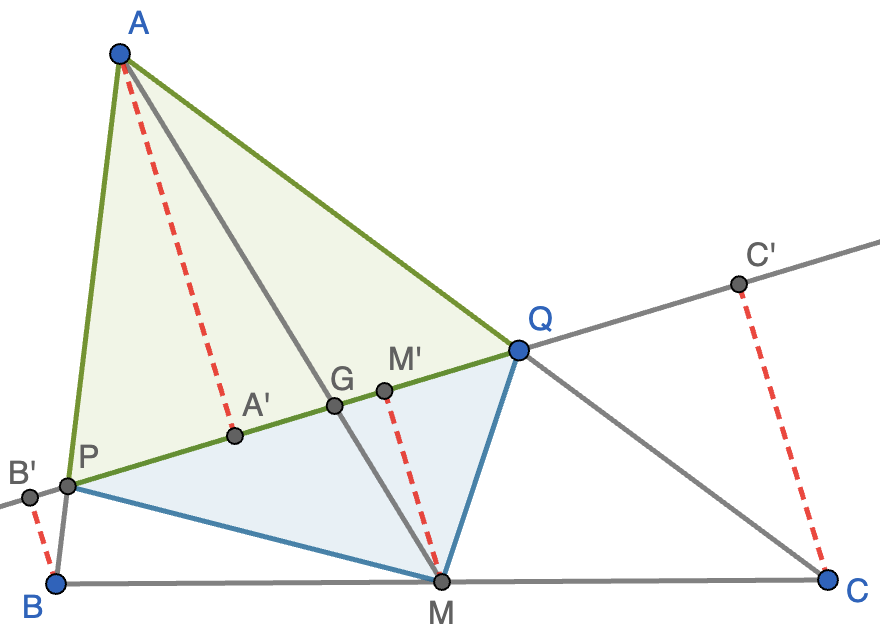
Solución. En primer lugar, nos damos cuenta de que $r$ no es una mediana y deja un vértice a un lado y dos al otro. Supondremos que es el vértice $A$ el que deja a un lado y $B$ y $C$ al otro. Sea $M$ el punto medio de $BC$, $G$ el baricentro y $P$ y $Q$ los puntos de corte de $r$ con los lados $AB$ y $BC$, respectivamente, como se muestra en la figura. También trazamos segmentos perpendiculares a $r$ por $A$, $B$, $C$ y $M$, que tienen sus pies en $A'$, $B'$, $C'$ y $M'$, respectivamente.
Sabemos que el baricentro divide a la mediana $AM$ en dos segmentos tales que $AG=2GM$, luego el triángulo $AGQ$ tiene doble de área del triángulo $GQM$ (tiene la misma altura y base doble) y el triángulo $AGP$ tiene el doble de área que el triángulo $PGM$. Por tanto, el área de $APQ$ (en verde) es también el doble que la de $PQM$ (en azul). Podemos calcular el área de $APQ$ como $\frac{1}{2}AA'\cdot PQ$ y el área de $PQM$ como $\frac{1}{2}MM'\cdot PQ$. Ahora nos damos cuenta de que $MM'=\frac{1}{2}(BB'+CC')$ por el teorema de Thales ya que $BB',MM',CC'$ son paralelas que cortan a $r$ y $BC$ con $BM=CM$. Por lo tanto, el área de $PQM$ es $\frac{1}{4}(BB'+CC')PQ$, que debe ser la mitad de $\frac{1}{2}AA'\cdot PQ$, luego necesariamente $AA'=BB'+CC'$, que es lo que queríamos demostrar.
Solución. Vamos a trabajar en coordenadas, escribiendo los vértices del triángulo como $(x_1,y_1)$, $(x_2,y_2)$ y $(x_3,y_3)$. Las coordenadas del baricentro son la media aritmética, es decir,
\[\left(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3}\right).\]
Por tanto, una recta que pasa por este punto tendrá ecuación $Ax+By+C=0$, siendo $A,B,C\in\mathbb{R}$ tales que $A^2+B^2\neq 0$ y
\[A\frac{x_1+x_2+x_3}{3}+B\frac{y_1+y_2+y_3}{3}+C=0.\]
Esto último puede reescribirse como
\[\frac{Ax_1+By_1+C}{3}+\frac{Ax_2+By_2+C}{3}+\frac{Ax_3+By_3+C}{3}=0.\]
Como las tres fracciones suman cero, habrá dos de ellas con un signo y otra con el signo opuesto (no pueden ser cero porque la recta no pasa por ningún vértice). Supondremos que las dos primeras son del mismo signo y la tercera del signo opuesto, luego tomando valores absolutos, dividiendo por $\sqrt{A^2+B^2}$ y multiplicando por $3$, tenemos
\[\frac{|Ax_1+By_1+C|}{\sqrt{A^2+B^2}}+\frac{|Ax_2+By_2+C|}{\sqrt{A^2+B^2}}=\frac{|Ax_3+By_3+C|}{\sqrt{A^2+B^2}}.\]
Cada fracción es la distancia desde el vértice correspondiente a la recta, luego el resultado está probado. El hecho de que dos fracciones tengan el mismo signo y otra el signo opuesto refleja el hecho de que la recta deja a dos puntos a un lado y al tercero al otro.

