Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 891
En un hexágono regular de lado unidad se sitúan $19$ puntos. Demuestra que
hay al menos un par de ellos separados por una distancia no mayor que $\frac{\sqrt{3}}{3}$.
pistasolución 1info
Pista. Descompón el hexágono en 18 regiones y utiliza el principio del palomar.
Solución. Consideramos la división del hexágono en 6 triángulos equiláteros de lado 1 indicada con líneas verdes en la figura y luego subdividimos cada triángulo en tres cometas uniendo su centro con los puntos medios de los tres lados, como se ha indicado con línea naranja. Esto nos da un total de 18 regiones y, por el principio del palomar, al menos 2 de los 19 puntos deben caer en una de ellas. Ahora bien, todas las regiones son congruentes entre sí y los puntos más distantes dentro de cada una de ellas son el centro y el vértice del triángulo equilátero en el que está contenida (véase la nota). Dicha distancia máxima es $\frac{2}{3}$ de la altura del triángulo, es decir, $\frac{2}{3}\cdot\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{3}$.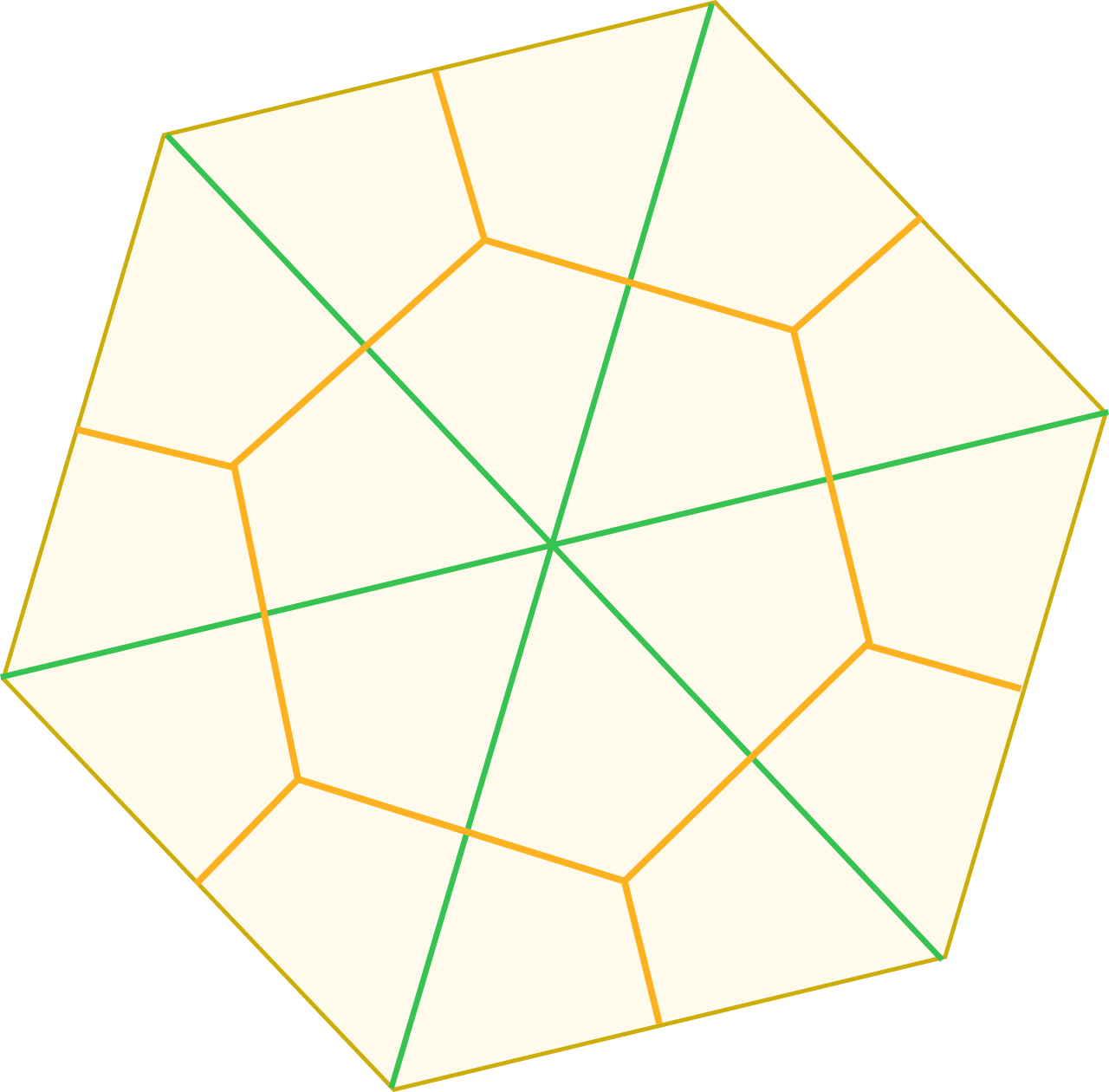

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre