Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 908
Sea $ABC$ un triángulo acutángulo con $\angle BAC=45^\circ$ y sea $P$ el pie de la altura que pasa por $B$. Trazamos la circunferencia de centro $P$ que pasa por $C$ y que vuelve a cortar a $AC$ en el punto $X$ y a la altura $PB$ en el punto $Y$. Sean $r$ y $s$ las rectas perpendiculares a la recta $AY$ por $P$ y $X$, respectivamente, y $L$ y $K$ las respectivas intersecciones de $r$ y $s$ con $AB$. Demostrar que $L$ es el punto medio de $KB$.
pistasolución 1info
Pista. Demuestra que $P$ es el ortocentro de $ABC$.
Solución. Como el triángulo $CXY$ es rectángulo isósceles, la recta $CY$ es perpendicular a $XY$ y por tanto también a $AB$ ($XY$ y $AB$ son paralelas ya que ambas forman un ángulo de $45^\circ$ con $AC$). Entonces, $CY$ es una altura del triángulo $ABC$ y, en consecuencia, $Y$ es el ortocentro del triángulo. En particular, deducimos que $AY$ es perpendicular a $CB$, luego $r$ y $s$ son paralelas a $CB$. Finalmente, el teorema de Thales nos asegura que $KL=LB$ a través de estas tres rectas paralelas ya que $XP=PC$.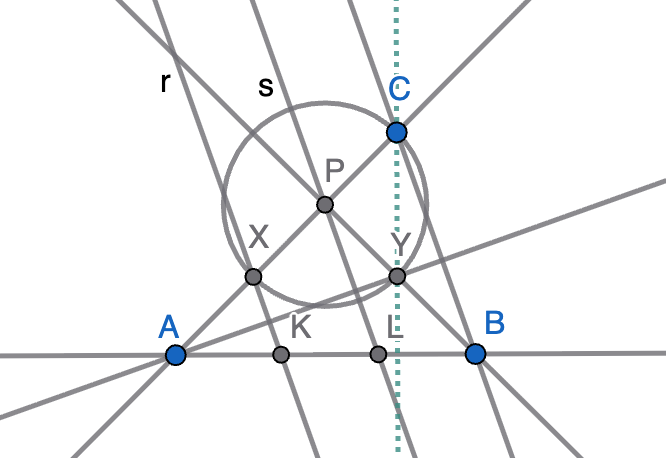

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre