Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
Llamamos $A$ al vértice con el ángulo recto, $B$ al vértice de $30^\circ$ y $C$ al de $60^\circ$. Sea $D$ el punto interior de $BC$ tal que $BE=\frac{3}{5}$ y trazamos la perpendicular a la hipotenusa $BC$ que pasa por $E$ y corta a $BC$ en otro punto $E$. Entonces, tenemos $ABC$ descompuesto como unión de los tres triángulos rectángulos $BDE$, $ACD$ y $BDE$, como se indica en la figura. Ahora bien, $BDE$ tiene hipotenusa $BD=\frac{3}{5}$, mientras que $ACD$ y $BDE$ comparten hipotenusa $CD$. El teorema de Pitágoras nos dice que
\begin{align*}
CD^2&=DA^2+AC^2=(AB-BD)^2+AC^2=(\mathrm{sen}(60)-\tfrac{3}{5})^2+\mathrm{cos}^2(60)\\
&=(\tfrac{\sqrt{3}}{2}-\tfrac{3}{5})^2+(\tfrac{1}{2})^2=\tfrac{34-15\sqrt{3}}{25}
\end{align*}
Tenemos que ver que este número es menor que $\frac{3}{5})^2=\frac{9}{25}$, lo que equivale a ver que $34-15\sqrt{3}\lt 9$ o, más simplificadamente, $5\lt 3\sqrt{3}$. Esto es inmediato ya que, elevando al cuadrado por ser números positivos, la desigualdad se reduce a $25\lt 27$.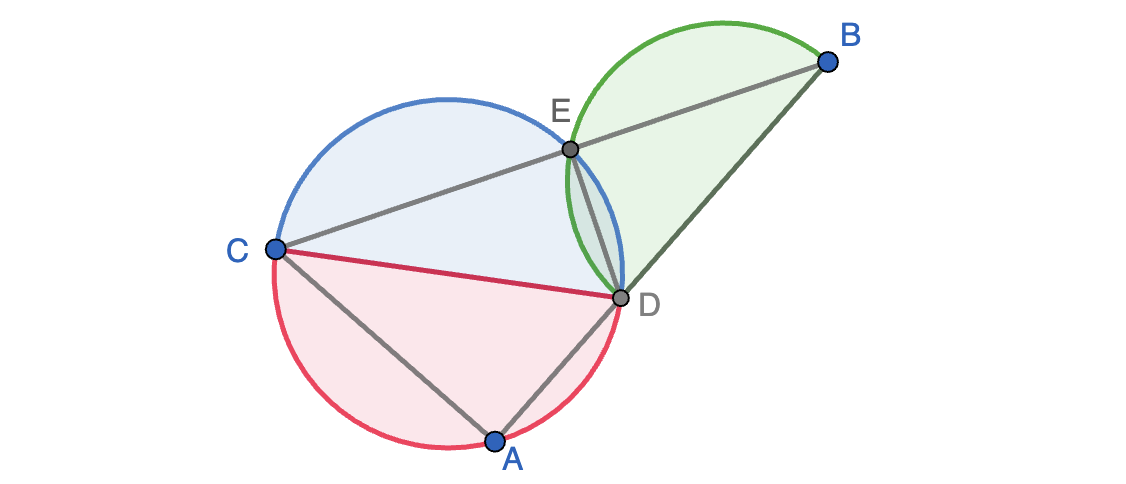
Informar de error en enunciado Informar de procedencia del problema