Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 961
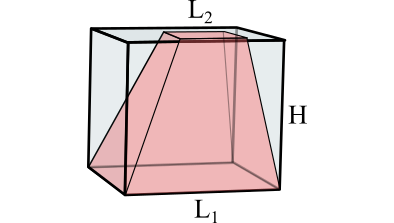
De un prisma recto de base cuadrada, con lado de longitud $L_1$ y altura $H$, extraemos un tronco de pirámide, no necesariamente recto, de bases cuadradas,
con lados de longitud $L_1$ (para la inferior) y $L_2$ (para la superior) y altura $H$. Si el volumen del tronco de pirámide es $\frac{2}{3}$ del total del volumen del prisma, ¿cuál es el valor de $\frac{L_1}{L_2}$?
pistasolución 1info
Pista. Calcula explícitamente el volumen de prisma y del tronco de pirámide en función de $H$, $L_1$ y $L_2$.
Solución. El volumen del prisma es $L_1^2H$. Si $H_T$ es la altura total de la pirámide (sin truncar), el volumen del prisma truncado se puede calcular restando al volumen de la pirámide sin trucar el volumen de la pirámide que se trunca. De esta manera, nos queda la ecuación
\[\frac{1}{3}(L_1^2H_T-L_2^2(H_T-H))=\frac{2}{3}L_1^2H,\]
de donde podemos despejar el valor de $x=\frac{L_1}{L_2}$ como
\[L_1^2(H_T-2H)-L_2^2(H_T-H)=0\ \Leftrightarrow\ x^2=\frac{L_1^2}{L_2^2}=\frac{H_T-H}{H_T-2H}=\frac{1-\frac{H}{H_T}}{1-2\frac{H}{H_T}}.\qquad(\star)\]
Por otro lado, podemos relacionar $H$ y $H_T$ mediante la sencilla proporcionalidad $\frac{L_1}{H_T}=\frac{L_2}{H_T-H}$, de donde podemos despejar también
\[x=\frac{L_1}{L_2}=\frac{H_T}{H_T-H}=\frac{1}{1-\frac{H}{H_T}}\ \Leftrightarrow\ \frac{H}{H_T}=1-\frac{1}{x}.\] Esta información la podemos sustituir directamente en $(\star)$:
\[x^2=\frac{1-(1-\frac{1}{x})}{1-2(1-\frac{1}{x})}=\frac{1}{2-x}.\]
Esto nos da la ecuación $x^3-2x+1=0$. Una solución es $x=1$, que debemos descartar ya que en tal caso $L_1=L_2$ y no se cumpliría el enunciado. Las otras dos soluciones son $x=\frac{1\pm\sqrt{5}}{2}$, de las que también podemos descartar la negativa ya que $x$ es el cociente de dos longitudes. Tenemos así que $\frac{L_1}{L_2}=\frac{1+\sqrt{5}}{2}$ es la razón áurea.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre