Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
I Olimpiada Matemática Española (fase nacional) — 1964
Sesión 1
- Determinar el intervalo en que debe mantenerse el número real $a$ para que las raíces de la ecuación sean imaginarias.
- Hallar el lugar geométrico de los puntos representativos de esas raíces en el plano complejo cuando $a$ recorre dicho intervalo.
Informar de error en enunciado Informar de procedencia del problema
- $f(x)$ es una función continua.
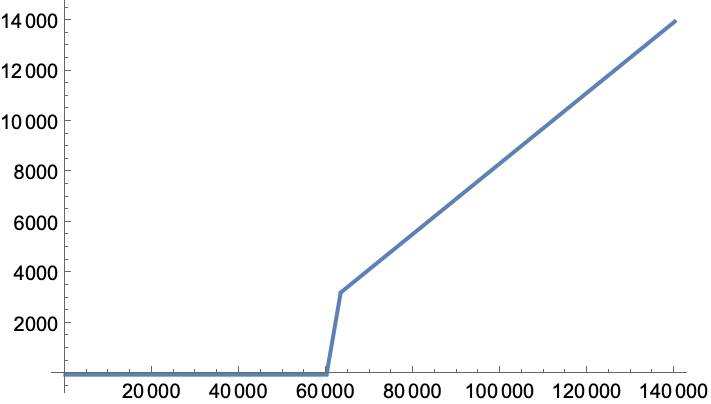
- La derivada $f'(x)$ en el intervalo $0\leq x\lt 60000$ es constante e igual a cero; en el intervalo $60000\lt x\lt P$ es constante e igual a $1$; y para $x\gt P$ es constante e igual a $0.14$.
- $f(0)=0$ y $f(140000) = 14000$.
Para representar la gráfica de la función, solo hay que darse cuenta de que está formada por tres trozos rectilíneos: el primero es la constante cero, el segundo tiene pendiente $1$ que pasa por el punto $(60000,0)$ y el tercero tiene pendiente $0.14$ y pasa por $(140000,14000)$. Queda así una gráfica como se muestra en la figura.
Informar de error en enunciado Informar de procedencia del problema
- El número de puntos de intersección de estas diagonales, excluidos los vértices.
- Cuántos de esos puntos son interiores al polígono.
Nota. Las fórmulas anteriores son válidas para un triángulo (los puntos de intersección interiores y exteriores son cero), aunque el razonamiento no es riguroso en este caso ya que estamos considerando números combinatorios que no están definidos como $\binom{0}{2}$ ó $\binom{3}{4}$.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Sesión 2
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Observando la sucesión de posiciones ocupadas por cada una de las fichas, demostrar que al cabo de 1000 operaciones análogas, aplicadas sucesivamente, el fichero vuelve a estar en su orden natural. Comprobar que no podría obtenerse un resultado análogo ($n$ operaciones para un fichero de $n$ fichas) si se tratase de un fichero con un número impar $n$ de fichas.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema