Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Sea $ABC$ el triángulo y $A'B'C'$ el triángulo rotado $90^\circ$, como se indica en la figura (estamos interesados en hallar el área de color naranja). Los seis triángulos pintados de azul son congruentes entre sí ya que las líneas discontinuas son ejes de simetría (¿por qué?). Consideramos los puntos de intersección $D$ y $E$ de $B'C'$ con $AC$ y $BD$, respectivamente. Tenemos entonces que $\angle DCE=\angle BCA=60^\circ$ y $\angle DEC=90^\circ$ porque $B'C'$ es una rotación de $90^\circ$ de $BC$. Por lo tanto, el triángulo $CDE$ es rectángulo y cumple que \[CE=CD\,\mathrm{sen}(30^\circ)=\tfrac{1}{2}CD,\qquad\qquad CE=CD\,\mathrm{cos}(30^\circ)=\tfrac{\sqrt{3}}{2}CD.\] Ahora usamos que $CD+DE+EC=C'D+DE+EB'=B'C'=4\sqrt{3}$ (ver la nota). Esto nos dice que \[\tfrac{1}{2}CD+CD+\tfrac{\sqrt{3}}{2}CD=4\sqrt{3}\ \Longleftrightarrow\ CD=\frac{8\sqrt{3}}{3+\sqrt{3}}.\] Por tanto, el área de cada triángulo azul será \[\text{Área}(CDE)=\frac{1}{2}DE\cdot EC=\frac{\sqrt{3}}{8}\left(\frac{8\sqrt{3}}{3+\sqrt{3}}\right)^2=8\sqrt{3}-12.\] Finalmente, el área que buscamos se calcula como el área de $ABC$, que es igual a $12\sqrt{3}$ (ver la nota), menos tres veces el área de $CDE$, luego el resultado es, en centímetros cuadrados: \[12\sqrt{3}-3\cdot (8\sqrt{3}-12)=36-12\sqrt{3}.\]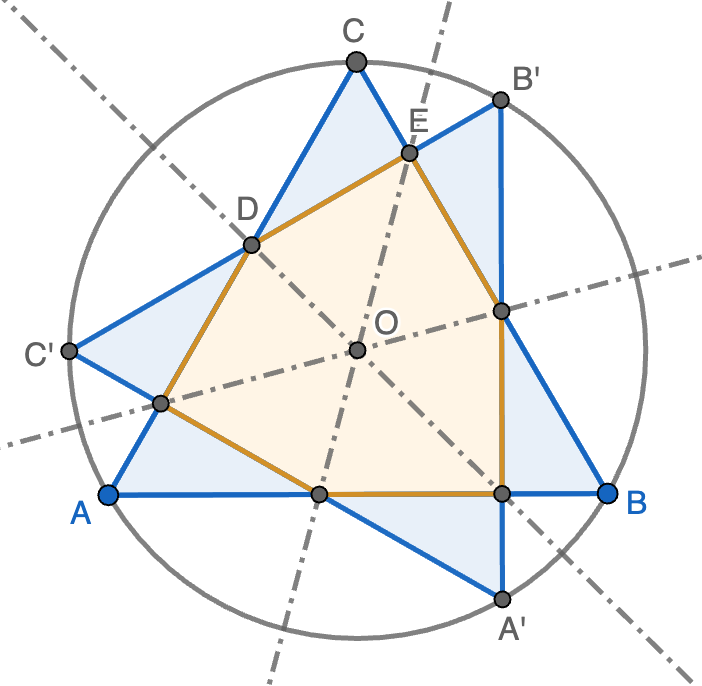

Nota. Hemos usado que si $\ell$ es el lado de un triángulo regular, entonces el radio de su circunferencia circunscrita es $R=\frac{\ell}{\sqrt{3}}$ y su área es $S=\frac{\sqrt{3}}{4}\ell^2$. ¿Sabrías probarlo?

Solución. Llamemos $a$ a la cifra de las cententas, $b$ a la de las unidades y $c$ a la de las unidades. Entonces, $b$ puede ser cualquier entero entre $2$ y $9$, $a$ tiene que estar entre $1$ y $b-1$ y $c$ entre $0$ y $b-1$. Por tanto, para cada valor de $b$ tenemos $(b-1)b=b^2-b$ posibles elecciones para el par $(a,c)$, por lo que la solución a la primera pregunta se obtiene sumando $b^2-b$ para $b$ desde $2$ a $9$, es decir, \begin{align*} 2^2+3^2+\ldots+9^2-(2+3+\ldots+9)&=1^2+2^2+\ldots+9^2-(1+2+\ldots+9)\\ &=\frac{9\cdot 10\cdot 19}{6}-\frac{9\cdot 10}{2}=240. \end{align*} Para responder al apartado (b), de lo anterior habrá que descontar los que tienen $a=c$, que ahora puede ser cualquier dígito entre $1$ y $b-1$, luego tendremos que la solución es \[240-(1+2+\ldots+8)=240-\frac{8\cdot 9}{2}=204.\]

Solución. El disco da $33\frac{1}{3}\times 24.5=\tfrac{100}{3}\times\frac{49}{2}=\tfrac{2450}{3}$ revoluciones en total, lo que nos da un ángulo de giro de $\tfrac{2450}{3}\times 2\pi=\frac{4900}{3}\pi$ radianes. La trayectoria del surco sigue una espiral de Arquímedes, que se parametriza en coordenadas polares como $r(\theta)=a\theta$, donde $a$ es el paso de la espiral.

Pongamos que el ángulo inicial es $\theta_i$ y el ángulo final es $\theta_f=\frac{4900}{3}\pi+\theta_i$, mientras que el radio inicial es $r_i=\frac{23}{4}$ y el radio final es $r_f=\frac{29}{2}$. Por lo tanto, debe cumplirse que \[\frac{23}{4}=a\theta_i,\qquad \frac{29}{2}=a\left(\frac{4900}{3}\pi+\theta_i\right).\] De este sistema de ecuaciones se deduce fácilmente que $\theta_i=\frac{3220}{3}\pi$ y $a=\frac{3}{560\pi}$, lo que nos da $\theta_f=\frac{8120}{3}\pi$. Entonces, la longitud del surco $L$ puede calcularse en coordenadas polares como la siguiente integral: \begin{align*} L&=\int_{\theta_i}^{\theta_f}\sqrt{r(\theta)^2+r'(\theta)^2}\,\mathrm{d}\theta=\int_{\frac{3220}{3}\pi}^{\frac{8120}{3}\pi}\sqrt{a^2\theta^2+a^2}\,\mathrm{d}\theta\\ &=\frac{3}{560\pi}\int_{\frac{3220}{3}\pi}^{\frac{8120}{3}\pi}\sqrt{1+\theta^2}\,\mathrm{d}\theta. \end{align*}

Esta última integral no es sencilla, pero puede resolverse mediante el cambio de variable $\theta=\operatorname{senh} t$, que nos lleva a $\mathrm{d}\theta=\cosh t$. Como $\cosh^2\theta=1+\operatorname{senh}^2\theta$, tenemos \begin{align*} \int\sqrt{1+\theta^2}\,\mathrm{d}\theta&=\int\cosh^2 t\,\mathrm{d}t=\int\frac{1+\cosh(2t)}{2}\,\mathrm{d}t\\ &=\tfrac{1}{2}t+\tfrac{1}{4}\sinh(2t)=\tfrac{1}{2}\operatorname{arcsenh}\theta+\tfrac{1}{4}\operatorname{senh}(2\operatorname{arcsenh}\theta). \end{align*} Por lo tanto, el resultado final será \[L=\frac{3}{560\pi}\left(\tfrac{1}{2}\operatorname{arcsenh}(\tfrac{8120}{3}\pi)+\tfrac{1}{4}\operatorname{senh}(2\operatorname{arcsenh}(\tfrac{8120}{3}\pi))-\tfrac{1}{2}\operatorname{arcsenh}(\tfrac{3220}{3}\pi)-\tfrac{1}{4}\operatorname{senh}(2\operatorname{arcsenh}(\tfrac{3220}{3}\pi))\right).\] Este último número puede hallarse con calculadora y nos da aproximadamente $51954,\!08930$ cm, es decir, aproximadamente $519,\!54$ m de longitud de surco.

Solución.

1. Si multiplicamos por $\cos(45)=\sin(45)=\frac{\sqrt{2}}{2}$ la ecuación, obtenemos \[\mathrm{sen}(x+45)=\mathrm{sen}(45)\cos(x)+\cos(45)\mathrm{sen}(x)=\mathrm{sen}(45)(\cos(x)+\mathrm{sen}(x)).\] Por lo tanto, la desigualdad que queremos probar se traduce en que \[\mathrm{sen}(x+45^\circ)\gt\cos(45).\] En el intervalo $[0,360]$, los ángulos cuyo seno es mayor que el seno de $45$ son los del intervalo $(45,135)$, luego la inecuación anterior tiene como soluciones los puntos de los intervalos $(0,90)$, salvo múltiplos de $360$.
2. Para $x\in(0,180)$, el seno es positivo, luego tenemos las mismas soluciones del apartado anterior $(0,90)$. Ahora bien, la función $f(x)=\cos(x)+|\mathrm{sen}(x)|$ cumple que $f(-x)=f(x)$ (es par), luego también tenemos las soluciones $(-90,0)$. Si observamos finalmente que $x=0$ no es solución ya que $f(0)=1$ y que $f(x)$ tiene período $360$, tenemos que la respuesta es los intervalos $(-90,0)$ y $(0,90)$, salvo múltiplos enteros de $360$.

Solución. Tenemos que \[\frac{3x-b}{3x-5b}=\frac{3a-4b}{3a-8b}\ \Longleftrightarrow\ (3x-b)(3a-8b)=(3a-4b)(3x-5b)\ \Longleftrightarrow\ b(x-a+b)=0.\] Por lo tanto, con la hipótesis de que ambas razones son iguales, necesariamente $b=0$ (en cuyo caso sí se tiene claramente que ambas son igual a $1$ y no hay paradoja) o bien $x-a+b=0$ (en cuyo caso la última igualdad no es $1$ ya que el denominador es cero y no puede hacerse el razonamiento).

En otras palabras, si $\frac{p}{q}=\frac{r}{s}$ entonces estas razones coinciden con $\frac{p-r}{q-s}$ con la condición adicional de que $q-s$ no sea cero.

Solución. Sea $ABC$ el triángulo equilátero, $M$ el punto medio del lado $AB$ y $O$ el centro de la esfera. El lado $AB$ es tangente a la esfera en $M$, luego perpendicular a $OM$, de forma que $AOM$ es un triángulo rectángulo y el teorema de Pitágoras nos asegura que \[AO^2=OM^2+MA^2=R^2+\frac{\ell^2}{4},\] luego la distancia que nos piden es $AO=\sqrt{R^2+\frac{\ell^2}{4}}$.

Solución. Sea $\rho$ el radio de la base menor y $h$ la altura del tronco de cono. Teniendo en cuenta que la altura del cono sin truncar es $mr$ y la del cono pequeño eliminado es $\rho m=rm-h$, se calcula fácilmente el volumen del tronco \[V=\frac{\pi}{3m^2}(m^3r^3-(mr-h)^3).\] Como la masa total es $Vd+\pi\rho^2p$, la función a maximizar es \[f(h)=\frac{\pi}{3m^2}(m^3r^3-(mr-h)^3)+\frac{\pi p}{m^2}(rm-h)^2.\] Esta función es un polinomio de tercer grado en $h$ cuya derivada viene dada por \[f'(h)=\frac{\pi}{m^2}(d(mr-h)^2-2p(mr-h)),\] que se anula cuando $h=mr$ o bien cuando $h=mr-\frac{2p}{d}$. Ahora bien, $f(h)$ es un polinomio de tercer grado con coeficiente líder positivo, luego tendrá un máximo relativo en $h=mr-\frac{2p}{d}$ y un mínimo relativo en $h=mr$. Además, se tiene la restricción $0\lt h\leq mr$ ya que la altura tiene que ser positiva y menor o igual que la del cono sin truncar. Se deduce así que

• Si $\frac{2p}{d}\lt mr$, la masa máxima se alcanza para $h=mr-\frac{2p}{d}$.
• En caso contrario, si $\frac{2p}{d}\geq mr$, la masa máxima se alcanza para $h=0$.

Solución. Sean $O_n$ y $r_n$ el centro y radio de la circunferencia $\gamma_n$, y sea $T_n$ su punto de tangencia con una de las dos rectas. Consideremos además la homotecia de razón $0\lt\lambda\lt 1$ con centro en $P$ que lleva $\gamma_1$ en $\gamma_2$. Es fácil ver entonces por inducción sobre $n$ que dicha homotecia lleva $\gamma_n$ en $\gamma_{n+1}$ para todo $n$, luego también lleva $O_n$ en $O_{n+1}$ y $T_n$ en $T_{n+1}$. En particular, tenemos que $r_n=\lambda^{n-1}r$ también por inducción sobre $n$. Ahora bien, la distancia $PO_1=a$ es la suma de $r$ y los diámetros de todas las circunferencias $\gamma_n$, es decir, \[a=r+2(r_2+r_3+\ldots)=r+2(\lambda r+\lambda^2r+\ldots)=r+2\lambda r(1+\lambda+\lambda^2+\ldots)=r+\frac{2\lambda}{1-\lambda},\] donde hemos usado la fórmula de la suma de una progresión geométrica infinita. De aquí podemos despejar $\lambda=\frac{a-r}{a+r}$ y podemos responder ya a los tres apartados:

1. El radio de $\gamma_2$ es $r_2=\lambda r=\frac{r(a-r)}{a+r}$.
2. El radio de $\gamma_n$ es $r_n=\lambda^{n-1}r=\frac{r(a-r)^{n-1}}{(a+r)^{n-1}}$.
3. El límite de la suma de las longitudes de las circunferencias es \[2\pi(r_1+r_2+\ldots)=2\pi r(1+\lambda+\lambda^2+\ldots)=\frac{2\pi r}{1-\lambda}=\pi(a+r).\]