Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
XII Olimpiada Matemática Española (fase nacional) — 1975
Sesión 1
Problema 1569problema obsoleto
Calcular el siguiente límite:
\[\lim_{n\to\infty}\frac{1}{n}\left(\frac{1}{n^k}+\frac{2^k}{n^k}+\ldots+\frac{(n-1)^k}{n^k}+\frac{n^k}{n^k}\right).\]
Recomendación: seguir el procedimiento de construcción de la integral.
pistasolución 1info
Pista. Seguir la recomendación viendo la expresión del enunciado como una suma de Riemann de la función $f(x)=x^k$.
Solución. Consideremos la función $f(x)=x^k$ en el intervalo $[0,1]$, el cual dividimos
\[[0,1]=[0,\tfrac{1}{n}]\cup[\tfrac{1}{n},\tfrac{2}{n}]\cup\ldots\cup[\tfrac{n-1}{n},1].\]
Entonces, se cumple que
\[\frac{1}{n}\left(\frac{1}{n^k}+\frac{2^k}{n^k}+\ldots+\frac{n^k}{n^k}\right)=\frac{1}{n}f\left(\tfrac{1}{n}\right)+\frac{1}{n}f\left(\tfrac{2}{n}\right)+\ldots+\frac{1}{n}f\left(\tfrac{n}{n}\right).\]
Cada uno de los sumandos anteriores es el área de un rectángulo de base $[\tfrac{m-1}{n},\tfrac{m}{n}]$ y altura $f(\tfrac{m}{n})$. Como $f(x)$ es creciente, se trata de la suma superior asociada a esta partición del intervalo $[0,1]$. En el proceso de construcción de la integral de Riemann se sabe que el límite de cualquier suma de Riemann (en particular, de la suma superior) de una función continua converge a la integral de la función en el intervalo. Por lo tanto, se cumple que
\[\lim_{n\to\infty}\frac{1}{n}\left(\frac{1}{n^k}+\frac{2^k}{n^k}+\ldots+\frac{n^k}{n^k}\right)=\int_0^1x^k\,\mathrm{d}x=\frac{1}{k+1}.\]
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1577problema obsoleto
Estudiar la función real
\[f(x)=\left(1+\frac{1}{x}\right)^x,\]
definida para $x\in\mathbb{R}-[-1,0]$. Representarla gráficamente.
pistasolución 1info
Pista. Estudia el dominio, los límites y la monotonía de $f(x)$.
Solución. En primer lugar, observamos que la función está bien definida salvo en los casos en que la base sea negativa o cero, es decir, su dominio es $\mathrm{Dom}(f)=\mathbb{R}-[-1,0]$ y es continua en todo su dominio por tratarse de una función elemental. Veamos algunas propiedades:

- Por tratarse de una función exponencial, $f(x)=e^{x\log(1+\frac{1}{x})}$ siempre es positiva.
- Los límites en $\pm\infty$ los obtenemos por definición del número $e$: \[\lim_{x\to+\infty}f(x)=\lim_{x\to-\infty}f(x)e.\] El límite en $x=0$ por la derecha nos da una indeterminación $\infty^0$, que podemos resolver como $e$ elevado al siguiente límite \[\lim_{x\to 0^+}\left(x\log(1+\frac{1}{x})\right)=\lim_{x\to 0^+}\frac{\log(1+\frac{1}{x})}{\frac{1}{x}}\stackrel{\mathrm{LH}}{=}\lim_{x\to 0^+}\frac{\frac{\frac{-1}{x^2}}{1+\frac{1}{x}}}{\frac{-1}{x^2}}=0,\] que hemos resuelto por la regla de L'Hôpital. Por lo tanto, $\lim_{x\to 0^+}f(x)=e^0=1$. El límite cuando $x$ tiende a $-1$ por la izquierda nos da $+\infty$ sin indeterminación.
- La derivada de $f(x)$ viene dada por \[f'(x)=\frac{\left(\frac{1}{x}+1\right)^x \left((x+1) \log \left(\frac{1}{x}+1\right)-1\right)}{x+1}\] cuyo signo es el signo de $\log(1+\frac{1}{x})-\frac{1}{x+1}$. Para estudiar este signo, hacemos el cambio de variable $t=1+\frac{1}{x}$, donde ahora el dominio de $t$ son los reales positivos, lo que nos da la función $g(t)=\log(t)+\frac{1}{t}+1$. Se tiene que $g'(t)=\frac{1}{t}-\frac{1}{t^2}=\frac{t-1}{t^2}$ y de aquí que $g(t)$ tiene un mínimo absoluto en $t=1$ (decrece en $(0,1)$ y crece en $(1,+\infty)$. Por lo tanto, $g(t)\geq g(1)=0$. Deducimos que $g(t)$ (y, por tanto, $f(x)$) es creciente en su dominio.
Con esta información y, si queremos, dando algunos valores enteros a $x$ para obtener mayor precisión, no es difícil dar un boceto de la gráfica de la función.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1578problema obsoleto
Designaremos por $Z_{(5)}$ un cierto subconjunto del conjunto $\mathbb{Q}$ de los números racionales. Un racional pertenece a $Z_{(5)}$ si y solo si se puede escribir como una fracción en la que el denominador no sea múltiplo de $5$. Por ejemplo, $13/10$ no pertenece a $Z_{(5)}$, ya que los denominadores de todas las fracciones iguales a $13/10$ son múltiplos de $5$; en cambio, $75/10$ pertenece a $Z_{(5)}$ ya que $75/10=15/12$.
- ¿Qué estructura algebraica (semigrupo, grupo, etc.) tiene $Z_{(5)}$ respecto de la suma?
- ¿Y respecto del producto?
- ¿Es $Z_{(5)}$ un subanillo de $\mathbb{Q}$?
- ¿Es $Z_{(5)}$ un $Z_{(5)}$-espacio vectorial?
pista
Sin soluciones
infoPista. Este es el mismo problema de la fase nacional de la Olimpiada Matemática Española de 1974.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1579
Probar que si el producto de $n$ números reales positivos es igual a $1$, entonces su suma es mayor o igual que $n$.
pistasolución 1info
Pista. Utiliza la desigualdad entre las medias aritmética y geométrica.
Solución. Se trata de la desigualdad entre las medias aritmética y geométrica ya que se cumple que
\[\frac{x_1+x_2+\ldots+x_n}{n}\geq \sqrt[n]{x_1x_2\cdots x_n}\]
para cualesquiera $x_1,x_2,\ldots,x_n\geq 0$. Si su producto es $1$, entonces su suma será mayor o igual que $n$.
Nota. Si no se quiere usar directamente la desigualdad, se puede adaptar a este caso concreto cualquiera de sus demostraciones.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Sesión 2
Problema 1580
En el plano tenemos una recta $r$ y dos puntos $A$ y $B$ que no pertenecen a $r$ pero se encuentran en el mismo semiplano determinado por ella. Determinar un punto $M$ de la recta tal que el ángulo de $r$ con $AM$ sea doble del de $r$ con $BM$ (considerando como ángulo de dos rectas el menor de los ángulos que forman).
pistasolución 1info
Pista. Intenta que $BM$ sea la bisectriz del ángulo que forman $r$ y $AM$ y procura no dejar ningún caso sin analizar.
Solución. Trazamos la circunferencia $\Gamma$ de centro $B$ que es tangente a $r$, la semicircunferencia de $\Gamma$ más distante de $r$ (marcada en azul en la figura superior) y la región entre dicha circunferencia y $r$ (marcada en rosa en la figura superior). También consideramos las semirrectas paralelas a $r$ que se proyectan fuera de $\Gamma$ (marcadas en verde en la figura superior). Distinguimos dos casos:
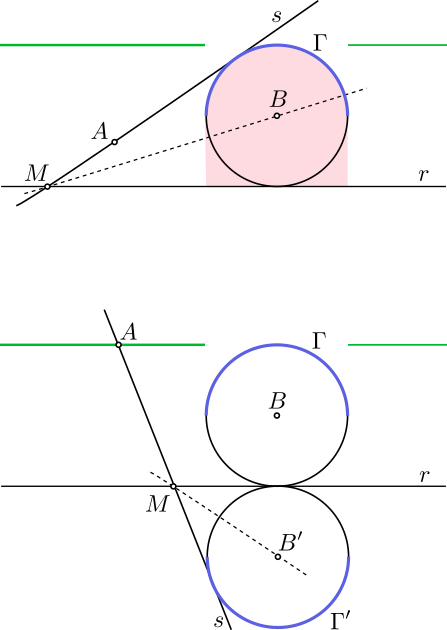
- Supongamos que $A$ no está en la región marcada en rosa. Entonces trazamos una recta tangente $s$ a $\Gamma$ que pase por $A$ y corte a $\Gamma$ en la semicircunferencia azul.
- Si $A$ no está en ninguna de las dos semirrectas paralelas a $r$ marcadas en verde, entonces podemos tomar $s$ que no sea paralela a $r$ y definimos $M$ como el punto de corte de $s$ y $r$. Entonces, $BM$ es la bisectriz del ángulo (menor de $90^\circ$) que forman $r$ y $AM$, luego se cumple la propiedad que queremos.
- Si $A$ está en una de las semirrectas marcadas en verde, entonces tomamos la circunferencia $\Gamma'$ simétrica de $\Gamma$ respecto de $r$ y $s$ una tangente a $\Gamma'$ en un punto de la semicircunferencia simétrica del original. Definimos de nuevo $M$ como el punto de corte de $s$ y $r$. Como $MB'$ es la bisectriz del ángulo menor de $90^\circ$ que forman $r$ y $s'$, se tiene que el ángulo que forman $MB$ y $r$ es igual al que forman $MB'$ y $r'$ y por tanto también se cumple la propiedad.
- Supongamos ahora que $A$ está en la región marcada de rojo. Entonces, las tangentes a $\Gamma$ o $\Gamma'$ son las únicas candidatas a cumplir la propiedad que deseamos y todas ellas la cumplen pero solo si consideramos el ángulo mayor que forman con $r$, no el menor como se especifica en el enunciado. Concluimos que en este caso el problema no tiene solución.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1581
Sean $\{x_n\}$ e $\{y_n\}$ dos sucesiones de números naturales definidas como
\begin{align*}
x_1&=1,&x_2&=1,& x_{n+2}&=x_{n+1}+2x_n\quad\text{ para todo }n\geq 1;\\
y_1&=1,&y_2&=7,& x_{n+2}&=2x_{n+1}+3x_n\quad\text{ para todo }n\geq 1.
\end{align*}
Demostrar que, salvo el caso $x_1=y_1=1$, no existe ningún número natural que aparezca en las dos sucesiones.
pistasolución 1info
Pista. Trabaja módulo $8$.
Solución. Los primeros términos de las sucesiones son
\begin{eqnarray*}
x_n:&\quad& 1,1,3,5,11,21,43,...\\
y_n:&\quad& 1,7,17,55,161,487,...
\end{eqnarray*}
Si calculamos los restos módulo 8, la sucesión queda
\begin{eqnarray*}
x_n\ (\text{mód}\ 8):&\quad& 1,1,3,5,3,5,3,5,...\\
y_n\ (\text{mód}\ 8):&\quad& 1,7,1,7,1,7,1,7,...
\end{eqnarray*}
Como cada resto sólo depende de los dos anteriores, en cuanto se repite una pareja de restos consecutivos, los demás restos se repiten periódicamente. Como el único resto que aparece en las dos sucesiones es el $1$, deducimos que cualquier número que aparezca en las dos tiene que ser congruente con $1$ módulo $8$, y a la vista de la primera sucesión sólo puede ser el propio $1$.
Nota. Este es el mismo problema que el problema 2 de la USA Mathematical Olympiad de 1973.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1582problema obsoleto
Se considera la función $f:\mathbb{R}\to\mathbb{R}$ definida por
\[f(x)=\frac{1}{|x+3|+|x+1|+|x-2|+|x-5|}.\]
- Determinar el máximo absoluto de $f(x)$.
- Representar la gráfica de $f(x)$.
pistasolución 1info
Pista. Escribe la función a trozos viendo en qué intervalos cada valor absoluto es positivo o negativo.
Solución. Los valores absolutos cambian signo en los puntos $-3$, $-1$, $2$ y $5$. Además, el denominador no se anula nunca (no pueden ser todos los valores absolutos iguales a cero simultáneamente), luego se trata de una función continua en todo $\mathbb{R}$. Podemos escribir la función a trozos como
\[f(x)=\begin{cases}
\frac{1}{-(x+3)-(x+1)-(x-2)-(x-5)}=\frac{1}{3-4x}&\text{si }x\leq -3,\\
\frac{1}{(x+3)-(x+1)-(x-2)-(x-5)}=\frac{1}{9-2x}&\text{si }-3\leq x\leq -1,\\
\frac{1}{(x+3)+(x+1)-(x-2)-(x-5)}=\frac{1}{11}&\text{si }-1\leq x\leq 2,\\
\frac{1}{(x+3)+(x+1)+(x-2)-(x-5)}=\frac{1}{7+2x}&\text{si }2\leq x\leq 5,\\
\frac{1}{(x+3)+(x+1)+(x-2)+(x-5)}=\frac{1}{-3+4x}&\text{si }5\leq x.\\
\end{cases}\]
También podemos calcular su derivada a trozos:
\[f(x)=\begin{cases}
\frac{4}{(3-4x)^2}\gt 0&\text{si }x\lt -3,\\
\frac{2}{(9-2x)^2}\gt 0&\text{si }-3\lt x\lt -1,\\
0&\text{si }-1\lt x\lt 2,\\
\frac{-2}{(7+2x)^2}\lt 0&\text{si }2\lt x\lt 5,\\
\frac{-4}{(3-4x)^2}\lt 0&\text{si }5\lt x.\\
\end{cases}\]
Por lo tanto, se trata de una función estrictamente creciente en $(-\infty,-1)$ y estrictamente decreciente en $(2,+\infty)$ (aunque no es derivable en $x=-3$ y $x=5$, la monotonía estricta se extiende a estos puntos por continuidad y porque las derivadas laterales son estrictamente positivas). Como $f(x)$ es constante en $[-1,2]$, deducimos que el máximo se alcanza en el todo este intervalo, donde el valor es $\frac{1}{11}$. Podemos además dar un bocento de la gráfica $y=f(x)$ teniendo en cuenta lo anterior y que $f(x)$ tiene límite cero en $\pm\infty$.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1583
Se eligen aleatoriamente dos números reales entre $0$ y $1$. Calcular la probabilidad de que uno cualquiera de ellos sea menor que el cuadrado del otro.
pistasolución 1info
Pista. Tomar dos números aleatorios entre $0$ y $1$ equivale a tomar un punto aleatorio de un cuadrado de lado $1$. Determina la probabilidad como el cociente entre el área de la región en la que se cumple la propiedad del enunciado y el área total del cuadrado.
Solución. Elegir aleatoriamente dos números reales $x$ e $y$ en el intervalo $[0,1]$ equivale a elegir un punto aleatorio del cuadrado de vértices $(0,0),(0,1),(1,0),(1,1)$, que tiene área $1$. Por lo tanto, la probabilidad que nos piden será el área de la región donde se cumple la propiedad que nos dan (dividido entre el área del cuadrado, que es $1$). La propiedad nos dice que $x\leq y^2$ o bien $y\leq x^2$; por simetría, el área será entonces dos veces el área entre la gráfica $y=x^2$ y el eje $OX$ en el intervalo $[0,1]$. Por lo tanto, la respuesta a la pregunta es
\[2\int_0^1x^2\,\mathrm{d}x=\frac{2}{3}.\]
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre