Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
XXIII Olimpiada Matemática Española (fase nacional) — 1987
Sesión 1
Problema 1656
Sean $a$, $b$ y $c$ las longitudes de los lados de un triángulo no isósceles. Se dan tres círculos concéntricos de radios $a$, $b$ y $c$.
- ¿Cuántos triángulos equiláteros de áreas distintas pueden construirse, de modo que las rectas que contienen sus lados sean tangentes a cada círculo?
- Hallar las áreas de dichos triángulos.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1657
Demostrar que para todo número natural $n\gt 1$ se cumple que
\[1\cdot\sqrt{\binom{n}{1}}+2\cdot\sqrt{\binom{n}{2}}+\ldots+n\cdot\sqrt{\binom{n}{n}}\lt\sqrt{2^{n-1}n^3}.\]
pistasolución 1info
Pista. Utiliza la desigualdad de Cauchy-Schwarz.
Solución. Aplicando la desigualdad de Cauchy-Schwarz a los vectores
\begin{align*}
u&=\left(\binom{n}{1}^{1/2},\binom{n}{2}^{1/2},\ldots,\binom{n}{n}^{1/2}\right),\\
v&=(1,2,\ldots,n),
\end{align*}
tenemos que
\begin{align*}
1\cdot\sqrt{\binom{n}{1}}+2\cdot\sqrt{\binom{n}{2}}+\ldots+n\cdot\sqrt{\binom{n}{n}}&\leq\sqrt{\binom{n}{1}+\binom{n}{2}+\ldots+\binom{n}{n}}\sqrt{1^2+2^2+\ldots+n^2}\\
&=\sqrt{2^n-1}\sqrt{\frac{n(n+1)(2n+1)}{6}}\\
&\lt\sqrt{2^n}\sqrt{\frac{2n^3}{6}}\lt \sqrt{2^n}\sqrt{\frac{n^3}{2}}=\sqrt{2^{n-1}n^3},
\end{align*}
donde hemos usado la fórmula para la suma de los $n$ primeros cuadrados y también que los elementos de la fila $n$-ésima del triángulo de Tartaglia suman $2^n$.
Nota. La desigualdad de Cauchy-Schwarz sobre dos vectores $u,v\in\mathbb{R}^n$ nos dice que \[|u_1v_1+u_2v_2+\ldots+u_nv_n|\leq (u_1^2+u_2^2+\ldots+u_n^2)^{1/2}(v_1^2+v_2^2+\ldots+v_n^2)^{1/2}\] y la igualdad se alcanza si y sólo si los vectores son proporcionales.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1658
Un triángulo dado $T$ se descompone en triángulos $T_1,T_2,\ldots,T_n$ de manera que:
- Ningún par de triángulos tiene puntos interiores comunes.
- La unión de todos los triángulos $T_i$ es $T$.
- Cada segmento que es lado de algún triángulo $T_i$, o bien es lado de otro triángulo $T_j$, o bien es lado del triángulo $T$.
pista
Sin soluciones
infoPista. Para el caso impar, utiliza la fórmula de Euler
caras + vértices = aristas + 2para el grafo plano formado por lados y vértices (observa que hay $n+1$ caras en dicho grafo).
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Sesión 2
Problema 451
Si $a$ y $b$ son números reales distintos, resolver el sistema
\[\left\{\begin{array}{l}
x+y=1,\\
(ax+by)^2\leq a^2x+b^2y.\end{array}\right.\]
Resolver también el sistema
\[\left\{\begin{array}{l}
x+y=1,\\
(ax+by)^4\leq a^4x+b^4y.\end{array}\right.\]
pistasolución 1info
Pista. Usa la desigualdad de Jensen con pesos $x$ e $y$, pero ten cuidado ya que los pesos pueden ser negativos. ¿Qué dice la desigualdad en tal caso?
Solución. La desigualdad de Jensen con pesos $x,y\geq 0$ tales que $x+y=1$, nos dice que si $f:\mathbb{R}\to\mathbb{R}$ es una función estrictamente convexa, entonces
\[f(ax+by)\leq xf(a)+yf(b).\]
ya que, en el intervalo $[a,b]$, la gráfica de la función se queda por debajo del segmento de recta que une los puntos $(a,f(a)$ y $(b,f(b))$. Ahora bien, fuera del intervalo $[a,b]$, la gráfica se queda por encima de la recta, lo que nos dice que, para $x,y\in\mathbb{R}$ tales que $x+y=1$, si uno de estos dos números es negativo, se cumple la desigualdad contraria:
\[f(ax+by)\gt xf(a)+yf(b).\]
Por ser un poco más explícitos en este punto, basta mirar la figura y tener en cuenta que:
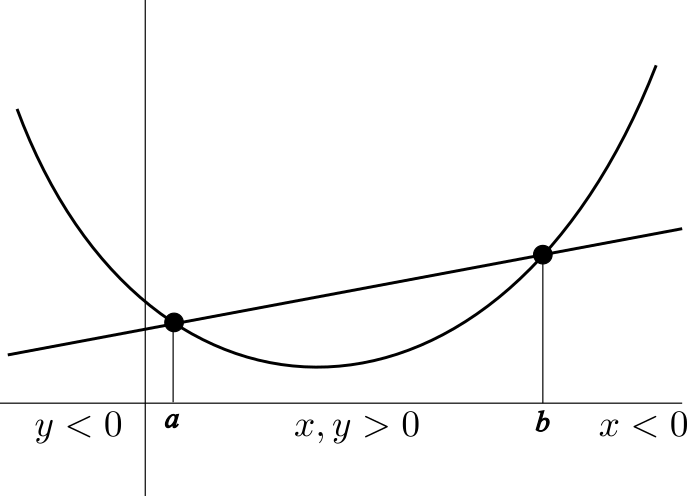
- Si $x+y=1$ y $a\lt b$, entonces el número $ax+by$ está entre $a$ y $b$ para $x,y\geq 0$, a la derecha de $b$ para $x\lt 0$ y a la izquierda de $a$ para $y\lt 0$.
- $f(ax+by)$ es el valor de la función en $ax+by$.
- $xf(a)+yf(b)$ es el valor de la recta en $ax+by$.
Aplicando este razonamiento a las funciones $f(t)=t^2$ y $f(t)=t^4$, que son ambas estrictamente convexas, deducimos que el conjunto de soluciones son los puntos $(x,y)$ que cumplen $x,y\geq 0$ y $x+y=1$. En otras palabras, son los puntos del segmento que une $(1,0)$ y $(0,1)$ en el plano.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1659
En un triángulo $ABC$ tenemos puntos $D$ y $E$ respectivamente sobre los lados $AB$ y $AC$. Conocemos la medida de los ángulos $\angle ABE=30^\circ$, $\angle EBC = 50^\circ$, $ACD = 20^\circ$ y $\angle DCB = 60^\circ$. Hallar el valor del ángulo $\angle EDC$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1660problema obsoleto
Para cada número natural $n$ se considera el polinomio $P_n(x)=x^{n+2}−2x+1$.
- Demostrar que la ecuación $P_n(x)=0$ tiene una raíz $c_n$ y sólo una en el intervalo $(0,1)$.
- Calcular $\lim_{n\to\infty}c_n$.
pista
Sin soluciones
infoPista. Utilizar el teorema de Bolzano y la monotonía de $P_n(x)$ en el intervalo $[0,1]$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre