Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
XXIX Olimpiada Matemática Española (fase nacional) — 1993
Sesión 1 — 26 de febrero de 1993
Informar de error en enunciado Informar de procedencia del problema
| 0 | 1 | 2 | 3 | 4 | $\cdots$ | 1991 | 1992 | 1993 | ||||||
| 1 | 3 | 5 | 7 | $\cdots$ | 3983 | 3985 | ||||||||
| 4 | 8 | 12 | $\cdots$ | 7968 |
Informar de error en enunciado Informar de procedencia del problema
Nota. Este no es un problema actual de olimpiada ya que apela a un resultado conocido como la desigualdad de Euler. De hecho, en la solución oficial, se menciona solamente que es consecuencia del teorema de Euler que nos dice que la distancia entre el incentro y el circuncentro de cualquier triángulo es $IO^2=R(R-2r)$.
Informar de error en enunciado Informar de procedencia del problema
Sesión 2 — 27 de febrero de 1993
- Si $p\neq 3$, entonces $\frac{10^{p-1}-1}{9}$ se escribe sólo con unos y es múltiplo de $p$.
- Si $p=3$, basta tomar $111=3\cdot 37$.
Informar de error en enunciado Informar de procedencia del problema
- ¿Cuántas figuras de 4 puntos existen con estas condiciones del enunciado?
- ¿Cuántas de ellas son geométricamente distintas (es decir, que no se deducen de otras por simetría)?
- Si representamos en coordenadas enteras según la cuadrícula $A=(x_1,y_1)=(1,1)$, $B=(x_2,y_2)$, $C=(x_3,y_3)$ y $D=(x_4,y_4)=(4,4)$, razonar que la suma \[\sum_{i,j=1}^4\left(|x_i-x_j|+|y_i-y_j|\right)\] es la misma para cualquiera de tales configuraciones de puntos $A,B,C,D$.

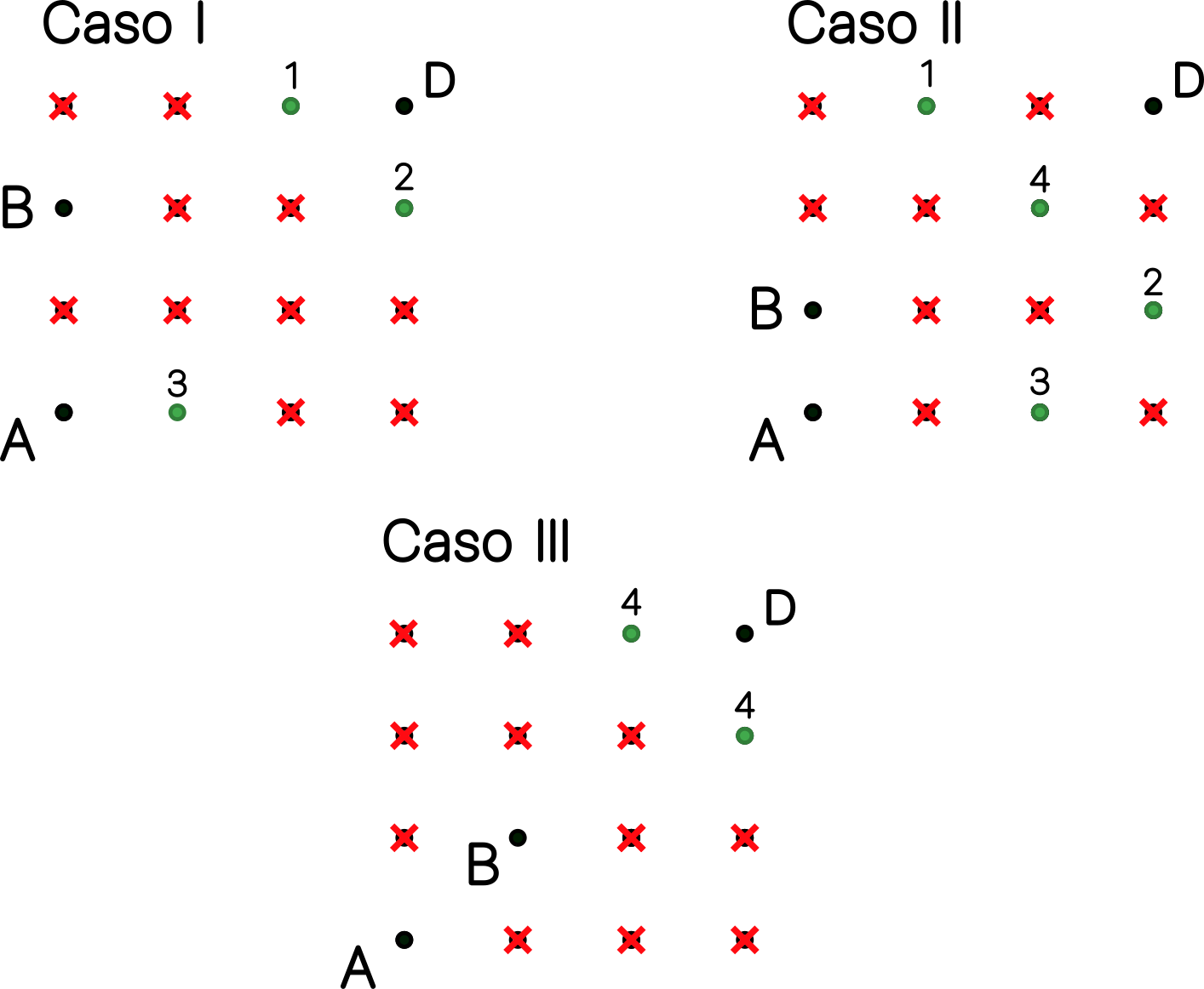
- En el caso I, hay 3 posiciones para $C$; como hay 4 posiciones de $B$ que producen el caso 1, tenemos un total de 12 configuraciones. En el caso II, hay 4 posiciones para $C$ para cada una de las cuatro posiciones para $B$, lo que nos da 16 configuraciones. En el caso III, tenemos 2 posiciones para C para cada una de las dos posiciones para $B$, lo que nos da 4 configuraciones. Tenemos así un total de $12+16+4=32$ configuraciones distintas de los puntos $B$ y $C$, que es la respuesta a (a).
- Para ver las que se obtienen salvo simetría, podemos restringirnos a las posiciones de $B$ de la figura. Ahora bien, se han marcado con números del 1 al 4 las posiciones de $C$ donde posiciones que comparten número son simétricas. Esto nos da la respuesta $4$ al apartado (b), ver la nota.
- Como los movimientos rígidos que estamos considerando conservan la cuadrícula, sólo habrá que analizar las configuraciones 1 a 4 dadas en el apartado (b) y ver que en todas ellas la suma $S$ del enunciado es la misma:
- Configuración 1: $S=2(1+3+3+2+2+0+2+3+3+1+1+0)=42$.
- Configuración 2: $S=2(2+2+3+0+1+1+0+3+3+3+3+0)=42$.
- Configuración 3: $S=2(0+2+3+2+3+1+0+1+3+1+3+2)=42$.
- Configuración 4: $S=2(1+2+3+1+2+1+1+3+3+2+2+0)=42$.
Nota. En el apartado (b) se ha considerado que dos conjuntos de 4 puntos son simétricos si se puede pasar de uno al otro por movimientos rígidos. A posteriori, se ha visto que la solución oficial contempla que el movimiento rígido conserve la etiqueta $A,B,C,D$ de los puntos, en cuyo caso hay 8 configuraciones.
Informar de error en enunciado Informar de procedencia del problema
- La bola vuelve a $S$ y entonces el jugador pierde.
- La bola llega a $G$ y entonces el jugador gana.

Nota. Este método, que puede parecer un poco sofisticado y mágico la primera vez que se ve, es el fundamento de lo que se conoce en teoría de la probabilidad como cadenas de Markov. Calcular directamente $p_A$ intentando entender el árbol de posibilidades es muy complejo.
Informar de error en enunciado Informar de procedencia del problema