Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
XXXII Olimpiada Matemática Española (fase nacional) — 1996
Sesión 1 — 22 de febrero de 1996
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
- Cuando decrece $f(0)$ mientras se fijan $f(-1)$ y $f(1)$.
- Cuando crece $f(1)$ mientras se fijan $f(-1)$ y $f(0)$.
- Cuando decrece $f(-1)$ mientras se fijan $f(0)$ y $f(1)$.
Por tanto, la parábola que toma los menores valores de $(-1,0)$ es aquella que cumple $f(-1)=f(0)=-1$ (mínimo posible) y $f(1)=1$ (máximo posible). Se obtiene fácilmente que esta parábola es $f(x)=x^2+x-1=(x+\frac{1}{2})^2-\frac{5}{4}$, lo que prueba que $f(x)\geq\frac{-5}{4}$ en $[-1,1]$ y hemos respondido así a la primera pregunta.
En cuanto a $g(x)$, comenzamos observando que \[g(x)=x^2(\tfrac{a}{x^2}+\tfrac{b}{x}+c)=x^2f(\tfrac{1}{x}).\] Por lo tanto, para acotar superiormente $|g(x)|$ en $[-1,1]$, tendremos que acotar inferiormente $|f(x)|$ en $(-\infty,-1]\cup[1,+\infty)$. Podemos seguir suponiendo que $a,b\geq 0$, luego $f(x)\geq f(-x)$ para $x\geq 1$ y solo debemos fijarnos en el caso $x\geq 1$. Un razonamiento similar al descrito más arriba nos dice que $f(x)$ crece para $x\in [1,+\infty)$ en cualquiera de las siguientes situaciones:
- Cuando decrece $f(0)$ mientras se fijan $f(-1)$ y $f(1)$.
- Cuando crece $f(1)$ mientras se fijan $f(-1)$ y $f(0)$.
- Cuando crece $f(-1)$ mientras se fijan $f(0)$ y $f(1)$.
Nota. La igualdad $|f(x)|=\frac{5}{4}$ sólo se alcanza en los siguientes casos: para los polinomios $f(x)=x^2+x-1$ y $f(x)=-x^2-x+1$ en $x=\frac{-1}{2}$ y para los polinomios $f(x)=x^2-x+1$ y $f(x)=-x^2+x-1$ en $x=\frac{1}{2}$. La igualdad $|g(x)|=2$ se alcanza sólo para los polinomios $g(x)=x^2-2$ y $g(x)=2-x^2$ en $x=0$.
Informar de error en enunciado Informar de procedencia del problema
Sesión 2 — 23 de febrero de 1996
Nota. Otra forma de ver la existencia y unicidad de solución (aunque no de calcularla) es usar el teorema de Bolzano. La función $f(t)=\sqrt{1-pt}+2\sqrt{1-t}-1$ es continua y estrictamente decreciente. Nos interesa su valor en $[0,\min\{1,\frac{1}{p}\}]$. Tenemos que $f(0)=2\gt 0$. Si $p\geq 1$, entonces evaluamos $f(\frac{1}{p})=2\sqrt{1-\frac{1}{p}}-1$, que es negativo si y sólo si $p\leq\frac{4}{3}$. Si $p\leq 1$, entonces $f(1)=\sqrt{1-p}-1$ es negativo siempre que $p\gt 0$. En resumen, tenemos que $0\leq p\leq \frac{4}{3}$ y que la solución es única.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
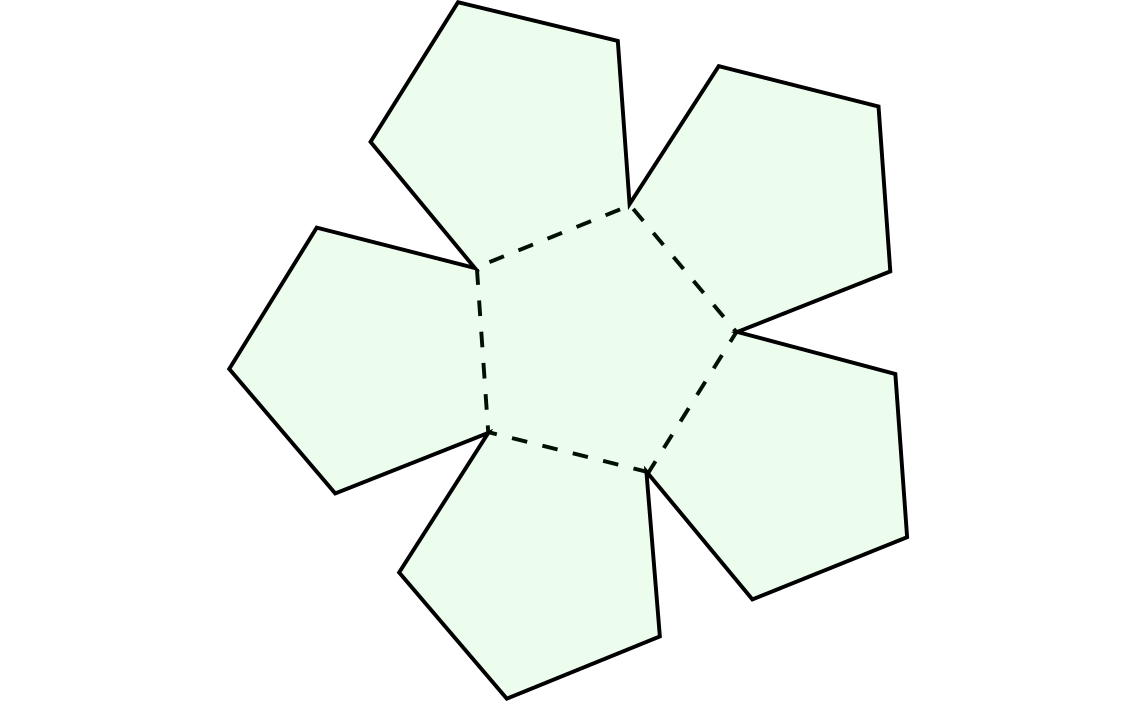
Informar de error en enunciado Informar de procedencia del problema