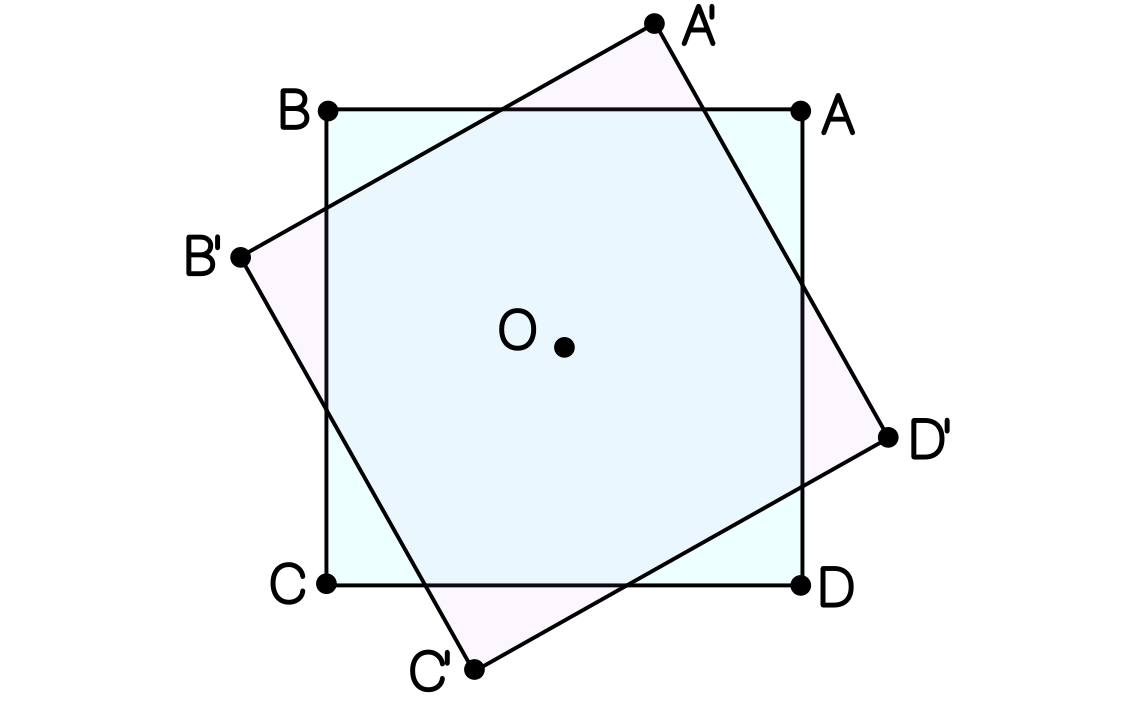
Un cuadrado $ABCD$ de lado $1$ gira un ángulo $\alpha$ en torno a su centro $O$. Hallar el área común a ambos cuadrados.
pistasolución 1info
Pista. El octógono se descompone en $8$ triángulos congruentes de altura $\frac{1}{2}$. Calcula la base correspondiente en términos de $\alpha$.
Solución. Consideremos los puntos $P$ y $Q$ indicados en la figura de abajo. Por simetría, el área se descompone en $8$ triángulos congruentes a $OPQ$. Este último triángulo, sombreado en la figura, tiene base $PQ$ y altura $\frac{1}{2}$, luego el área que nos piden es $S=8\cdot\frac{1}{2}\cdot\frac{1}{2}\cdot PQ=2 PQ$ y será suficiente calcular la longitud de $PQ$ en función de $\alpha=\angle A'PQ$.
Por la simetría de la figura y usando trigonometría en el triángulo $A'PQ$, obtenemos que $BP=A'P=PQ\cos\alpha$. Análogamente, tenemos que $AQ=A'Q=PQ\operatorname{sen}\alpha$, con lo que
\[1=AB=AQ+PQ+BP=PQ(1+\operatorname{sen}\alpha+\cos\alpha).\]
Esto nos lleva a la solución del problema
\[S=2PQ=\frac{2}{1+\operatorname{sen}\alpha+\cos\alpha}.\]
Nota. La solución presupone que $\alpha\in[0,90]$ implícitamente. Para un valor de $\alpha$ general, por la simetría de la construcción basta reducirlo módulo $90$ a un ángulo de dicho intervalo.
Determinar todos los números naturales de cuatro cifras que sean iguales al cubo de la suma de sus cifras.
pistasolución 1info
Pista. Si un número es igual al cubo de la suma de sus cifras, entonces tiene que ser un cubo perfecto, ¿no?
Solución. La forma más sencilla de resolver este problema darse cuenta de que el número en cuestión tiene que ser un cubo perfecto de 4 cifras y, por tanto, tiene que ser el cubo de un número entre 10 y 21. En este punto, podría probarse caso por caso y llegar a la solución, aunque vamos a ver que podemos descartar algunos números directamente.
Es bien sabido que la suma de las cifras tiene el mismo resto que el propio número módulo $9$ luego si llamamos $r$ a dicho resto, ha de cumplirse que $r\equiv r^3\ (\text{mód }9)$, es decir, $r\equiv -1$, $r\equiv 0$ ó $r\equiv 1\ (\text{mód }9)$. Esto nos lleva a que el número es el cubo de 10, 17, 18 ó 19. Probando cada uno de estos cuatro casos llegamos a que los únicos que cumplen la condición son $17^3=4913$ y $18^3=5832$.
Sea $ABC$ un triángulo. Consideremos los puntos $D$ y $E$ sobre el lado $BC$ de forma que las rectas $AD$ y $AE$ son paralelas a las tangentes a la circunferencia circunscrita al triángulo que pasan por $C$ y $B$, respectivamente. Demostrar que
\[\frac{BE}{CD}=\frac{AB^2}{AC^2}.\]
pistasolución 1info
Pista. Si tomamos la paralela a $BC$ que pasa por $A$ y llamamos $P$ y $Q$, respectivamente, a los puntos de corte de esta recta con la tangente por $B$ y con la tangente por $C$ definidas en el enunciado, demuestra que $ABC$, $ABP$ y $ACQ$ son semejantes.
Solución. Consideremos la recta paralela a $BC$ que pasa por $A$ y llamamos $P$ y $Q$, respectivamente, a los puntos de corte de esta recta con la tangente por $B$ y con la tangente por $C$ definidas en el enunciado. Entonces, se cumple que $BE=AP$ y $CD=AQ$, ya que los cuadriláteros $APBE$ y $AQCD$ son paralelogramos. Si denotamos por $\alpha,\beta,\gamma$ los ángulos del triángulo $ABC$, el paralelismo de $PQ$ y $BC$ también nos asegura que $\angle PAB=\beta$ y $\angle QAC=\gamma$. Por otro lado, como $\angle ACQ$ es el ángulo semiinscrito correspondiente y $AC$ está abarcado por el ángulo $\angle ABC=\beta$, se sigue que $\angle ACQ=\beta$ y, de la misma forma, $\angle ACQ=\gamma$. Así, hemos probado que los triángulos $ABC$, $ABP$ y $ACQ$ son semejantes. Por tanto, $AP/AB=AB/BC$ y $AQ/AC=AC/BC$, luego despejamos $BE=AP=AB^2/BC$ y $CD=AQ=AC^2/BC$, y obtenemos fácilmente la identidad del enunciado.
Hallar las tangentes de los ángulos de un triángulo sabiendo que son números enteros positivos.
pistasolución 1info
Pista. Prueba en primer lugar que una de las tangentes tiene que ser igual a $1$. ¿Qué pasaría si todas fuesen mayores o iguales que $2$?
Solución. Al ser las tangentes enteros positivos, deducimos que los tres ángulos del triángulo son agudos de al menos $45^\circ$. Ahora bien, no puede ser todas las tangentes mayores o iguales que $2$ ya que entonces la suma de los ángulos del triángulo sería mayor o igual que $3\arctan(2)\gt 3\arctan(\sqrt{3})=180^\circ$, donde hemos usado que el arcotangente es una función creciente. Deducimos que uno de los tres ángulos tiene que tener tangente igual a $1$ y, por tanto, ser igual a $45^\circ$. Si llamamos $\alpha$ y $\beta$ a los otros dos ángulos, tendremos que $\alpha+\beta=135^\circ$, luego
\[-1=\tan(135^\circ)=\tan(\alpha+\beta)=\frac{\tan(\alpha)+\tan(\beta)}{1-\tan(\alpha)\tan(\beta)},\]
igualdad que se puede reescribir como
\[\tan(\alpha)\tan(\beta)-\tan(\alpha)-\tan(\beta)=1\]
o bien
\[(\tan(\alpha)-1)(\tan(\beta)-1)=2.\]
La única posibilidad siendo las tangentes enteros positivos es que uno de los factores sea igual a $1$ y el otro igual a $2$, luego podemos suponer que $\tan(\alpha)=2$ y $\tan(\beta)=3$. Tenemos así que las tangentes de los tres ángulos son los números $1$, $2$ y $3$.
Nota. Observemos que el propio cálculo anterior nos dice que $\tan(\alpha+\beta)=-1$, luego $\alpha=\arctan(2)$ y $\beta=\arctan(3)$ suman $135^\circ$. Esto nos lleva directamente a la famosa identidad
\[\arctan(1)+\arctan(2)+\arctan(3)=180^\circ.\]
Hallar todas las funciones $f:\mathbb{N}\rightarrow\mathbb{N}$ estrictamente crecientes y tales que, para todo $n\in\mathbb{N}$,
\[f(n+f(n))=2f(n).\]
pistasolución 1info
Pista. Si llamamos $f(1)=a$, ¿qué puedes deducir del hecho de que $f(a+1)=2a$? Piensa que la función es estrictamente creciente, es decir, si $n\gt m$, entonces $f(n)\gt f(m)$.
Solución. Si llamamos $f(1)=a$, la ecuación del enunciado nos dice que $f(a+1)=2a$. Como $f$ es estrictamente creciente, y en los intervalos $[1,a+1]$ y $[a,2a]$ hay exactamente $a$ números enteros, deducimos que $f(2)=a+1$, $f(3)=a+2$,... hasta $f(a+1)=2a$. En otras palabras, $f(n)=a-1+n$ siempre que $1\leq n\leq a+1$. Sustituyendo ahora $n=a+1$ en la ecuación del enunciado, tenemos que $f(3a+1)=4a$ y, como hay $2a+1$ números tanto en el intervalo del dominio $[a+1,3a+1]$ como en el de la imagen $[2a,4a]$, deducimos que $f(a+2)=2a+1$, $f(a+3)=2a+2$,... hasta $f(3a+1)=4a$, luego $f(n)=a-1+n$ siempre que $1\leq n\leq 3a+1$. Repitiendo el proceso se deduce que $f(n)=a-1+n$ para todo $n\in\mathbb{N}$, de donde deducimos que toda función que cumpla el enunciado ha de ser de esta forma. Como estas funciones lo cumplen (¡comprobarlo!), deducimos que son las únicas.
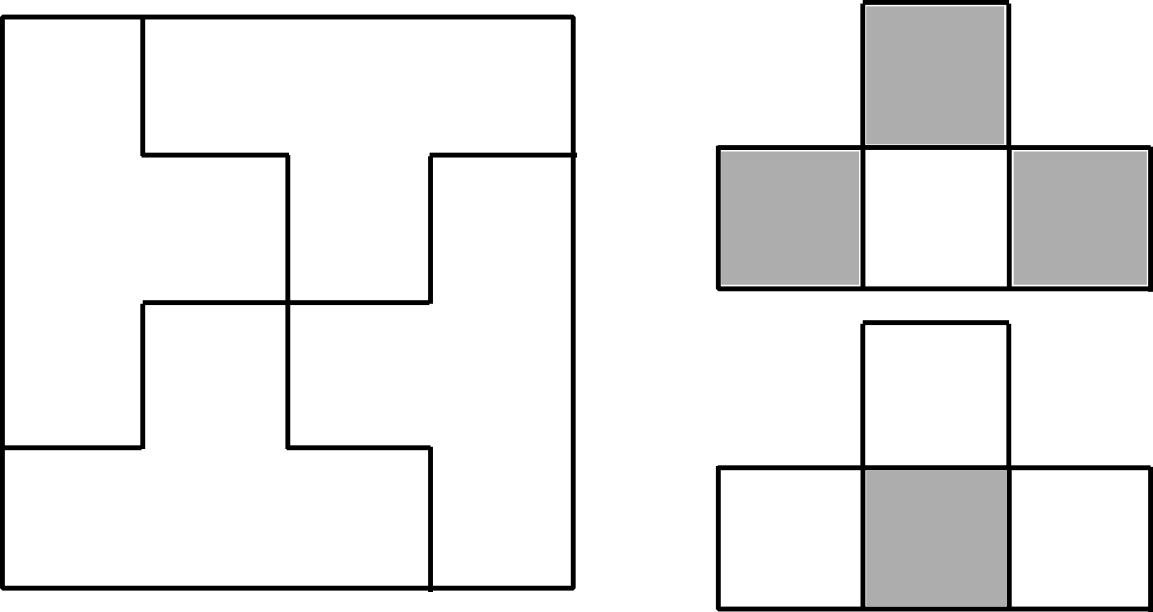
Determina los valores de $n$ para los que es posible construir un cuadrado $n\times n$ ensamblando tetrominós como el de la figura (formado por cuatro cuadraditos $1\times 1$).

pistasolución 1info
Pista. Colorea el cuadrado como un tablero de ajedrez.
Solución. Lo primero que observamos es que si $n$ es impar, entonces el tablero tiene un número impar de casillas y no se puede rellenar con un número entero de fichas, cada una de las cuales ocupa cuatro casillas. Por tanto, supondremos que es par en lo que sigue. Distingamos dos casos:
- Si $n=4k$, entonces el cuadrado se puede construir. Para ello, basta descomponerlo en cuadrados $4\times 4$ (mediante rectas paralelas a los lados del cuadrado y rellenar cada uno de ellos con cuatro tetrominós como se indica en la figura de la izquierda.
- Si $n=4k+2$, vamos a probar que el cuadrado no se puede construir. Para ello, coloreamos el cuadrado como un tablero de ajedrez, alternando colores blanco y negro en casillas adyacentes. Cada tetrominó ocupa o bien tres casillas blancas y una negra o bien tres negras y una blanca (como los que se indican en la figura de la derecha). Llamamos $a$ al número de tetrominós del primer tipo y $b$ al del segundo tipo en un supuesto ensamblado. Como hay el mismo número de casillas blancas que negras ($n$ es par), se sigue que $a+b$ es par, luego $n^2=4(a+b)$ es múltiplo de $8$. Esto no es posible si $n=4k+2$, luego el ensamblado es imposible.