Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Supongamos que los puntos son $A=(a,a^2)$ y $B=(b,b^2)$ con $a\lt b$. Teniendo en cuenta que la derivada de $x^2$ es $2x$, podemos calcular las expresiones $y=2ax-a^2$ e $y=2bx-b^2$ de las rectas tangentes. Es fácil resolver el sistema para obtener que estas tangentes se cortan en el punto $C=(\frac{a+b}{2},ab)$. Por otro lado, el punto medio de $AB$ es $M=(\frac{a+b}{2},\frac{a^2+b^2}{2})$, luego la recta $CM$ tiene ecuación $x=\frac{a+b}{2}$ (se trata de una recta vertical). El área de $ABC$ es el área de $BCM$ más el área de $ACM$, que pueden calcularse como un medio de la mediana $m=CM$ por las alturas respecto de este lado, que son rectas horizontales. Estas alturas son, de hecho, la diferencia de las primeras coordenadas de $B$ y $M$ y de $A$ y $M$. Tenemos entonces que el área que nos piden es \[\mathrm{Área}(ABC)=\mathrm{Área}(BCM)+\mathrm{Área}(ACM)=\tfrac{1}{2}m(b-\tfrac{a+b}{2})+\tfrac{1}{2}m(\tfrac{a+b}{2}-a)=\tfrac{1}{2}m(b-a).\] Ahora bien, tenemos también que $m=\frac{a^2+b^2}{2}-ab=\frac{1}{2}(b-a)^2$, de donde podemos despejar $b-a=\sqrt{2m}$. Con todo esto, podemos expresar el área únicamente en función de $m$ como nos piden: \[\mathrm{Área}(ABC)=\frac{\sqrt{2}}{2}m^{3/2}.\]

Solución. Tomamos $a_1=3$. Para $n\geq 2$, si suponemos que $a_1^2+a_2^2+\ldots+a_{n-1}^2$ es un cuadrado impar, entonces es de la forma $4k+1$ y podemos definir $a_n=2k$ de forma que $a_1^2+a_2^2+\ldots+a_n^2=(4k+1)+4k^2=(2k+1)^2$ también es un cuadrado impar.

Nota. De hecho, el método permite construir explícitamente tantos términos de la sucesión como queramos. Por ejemplo, los primeros serán \[\{3,4,12,84,3612,6526884,\ldots\}\]

Solución. Cada casilla es vecina de un número par de fichas (las del interior tienen 6 vecinas, las de los lados tienen 4 y las de los vértices tienen 2). Por tanto, si una ficha concreta resulta ser la última en retirarse, antes hemos tenido que quitar todas sus vecinas, lo que supone un número par de cambios de color. Esto nos dice que al proceder a retirar la última, su color es blanco y no puede retirarse. La respuesta a la pregunta del enunciado es, por tanto, negativa.

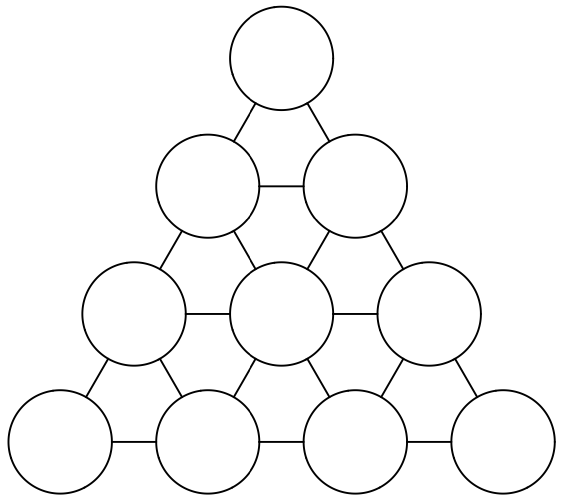
Nota. ¿Se pueden retirar todas las fichas menos una?

Solución. Observemos que la suma mínima corresponde al número 100 y la máxima al número 999. Por lo tanto, las sumas varían entre 1 y 27 y hacen un total de 27 sumas distintas, pero las sumas 1 y 27 sólo se tienen en las tarjetas correspondientes a 100 y 999, respectivamente. En consecuencia, el mayor número de tarjetas posible sin tener tres de igual suma es 52 (2 correspondientes a las tarjetas 100 y 999 y dos correpondientes a cada suma entre 2 y 26. De esto deducimos que si tomamos 53 tarjetas cualesquiera, siempre habrá tres que tengan la misma suma.

Solución. Si denotamos por $h_a$ a la longitud de la altura sobre el lado $a$, por aplicación sencilla del teorema de Thales tenemos que $g_a=\frac{1}{3}h_a$, ya que el baricentro divide a la mediana en dos segmentos, uno de longitud doble que el otro. Ahora bien, si $S$ es al área del triángulo y $p$ su semiperímetro, sabemos que se cumple que $S=\frac{1}{2}ah_a=rp$, de donde \[g_a=\frac{1}{3}h_a=\frac{2S}{3a}=\frac{2r}{3}\cdot\frac{p}{a}.\] Como $p-a=\frac{1}{2}(-a+b+c)\geq 0$ por la desigualdad triangular, deducimos que $\frac{p}{a}\geq 1$. Por tanto, la identidad anterior nos dice que $g_a\geq\frac{2r}{3}$ y, análogamente, se prueban las otras dos desigualdades del apartado (a).

Para el apartado (b), observemos que no es suficiente sumar las tres desigualdades ya obtenidas, sino que hay que trabajar un poco más. Usando lo que ya hemos calculado y la desigualdad entre las medias aritmética y armónica llegamos a que \[\frac{1}{r}(g_a+g_b+g_c)=\frac{2p}{3}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\geq\frac{2p}{3}\left(\frac{9}{a+b+c}\right)=\frac{18p}{6p}=3.\]

Nota. En realidad, para que se dé la igualdad en alguna de las desigualdades del apartado (a) tiene que ocurrir que $p=a$, $p=b$ ó $p=c$, para lo que el triángulo $ABC$ tendría que ser degenerado. Por tanto, podría decirse que las desigualdades del apartado (a) son estrictas. Por el contrario, la igualdad en la desigualdad del apartado (b) se alcanza cuando el triángulo es equilátero, como puede deducirse de la igualdad en la desigualdad de las medias.

Solución. Sean $a$, $b$ y $c$ el número de rectas en cada familia. La primera familia divide al plano en $a+1$ regiones y, al añadirle la segunda familia, dividen al plano en $(a+1)(b+1)$ regiones. Ahora bien, cada recta de la tercera familia corta a las otras $a+b$ rectas de las dos primeras, luego corta a $a+b+1$ regiones. En otras palabras, cada una de las $c$ rectas de la tercera familia produce $a+b+1$ nuevas regiones, por lo que el número total de regiones que delimitan las tres familias juntas está dado por \[n=(a+1)(b+1)+c(a+b+1)=a+b+c+ab+bc+ac+1.\] Llamemos $s=a+b+c$ al número total de rectas y acotemos $n$ en función de $s$. Para ello, observamos que \[s^2=a^2+b^2+c^2+2(ab+bc+ac)\geq 3(ab+bc+ac)\] ya que la desigualdad de reordenación nos asegura que $a^2+b^2+c^2\geq ab+bc+ac$. Deducimos que \[n\leq s+\frac{s^2}{3}+1.\] El miembro de la derecha es una función creciente de $s$ y \[s+\frac{s^2}{3}+1=1999 \Leftrightarrow\ s=\frac{3}{2}(-1+\sqrt{2665})\approx 75,94\] (nos quedamos sólo con la solución positiva). Por tanto, si $s\leq 75$ el número máximo de regiones es menor o igual que $1999$, luego el número buscado es $s\geq 76$. Para ver que $s=76$ es válido, busquemos un ejemplo. Tomando $a=24$, $b=26$ y $c=26$ obtenemos que \[n=24+26+26+24\cdot 26+26\cdot 26+24\cdot 26+1=2001\gt 1999,\] luego el mínimo número de rectas necesarias es $76$.