Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
LVIII Olimpiada Matemática Española (fase nacional) — 2022
Sesión 1 — 1 de abril de 2022
Problema 601
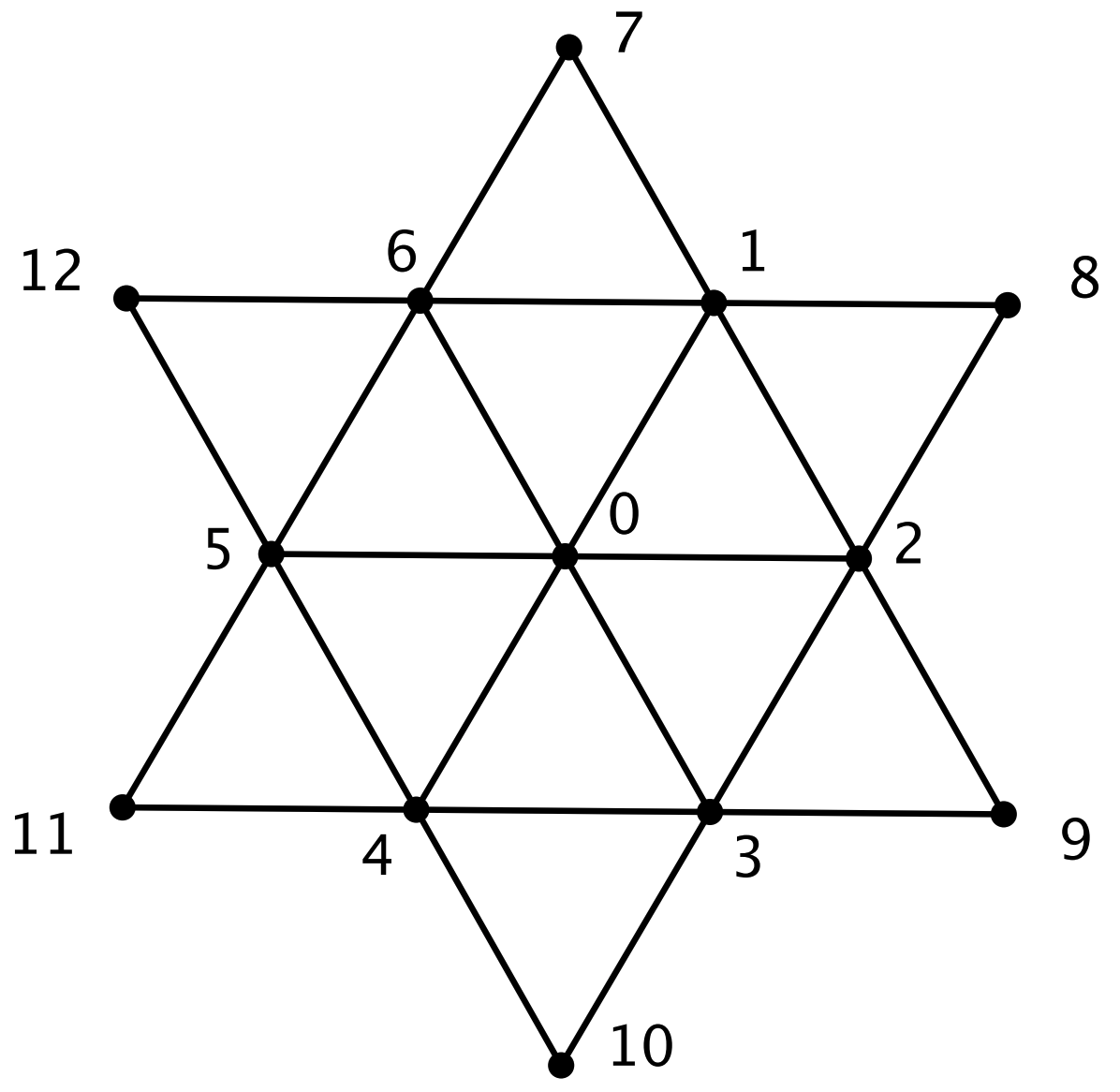
La estrella de seis puntas de la
figura es regular: todos los ángulos interiores de los triángulos pequeños son iguales. A cada uno de los trece puntos señalados se le asigna un color: verde o rojo. Demuestra que siempre habrá tres puntos del mismo color que son vértices de un triángulo equilátero.
pistasolución 1info
Pista. Fíjate en el triángulo de vértices $0,1,2$ y distingue casos según el color de sus vértices.
Solución. Tomemos el triángulo de vértices $0,1,2$ y supongamos que no tiene sus tres vértices del mismo color, luego tiene dos de un color (que supondremos es el verde) y otro del otro color (rojo). Tenemos dos casos, dependiendo de si los dos verdes son $0$ y $1$ o bien $1$ y $2$ (el caso en el que son $0$ y $2$ es simétrico).
- Si $0$ y $1$ son verdes, entonces $2$ y $6$ son rojos, luego $4$ es verde y $3$ y $5$ son rojos. En consecuencia, $9$ y $12$ son verdes y tenemos el triángulo equilátero de vértices $1,4,9$ con sus tres vértices verdes.
- Si $1$ y $2$ son verdes, entonces $0$ y $8$ son rojos, luego $7$ y $9$ son verdes. Por tanto, $3$, $4$, $5$, $6$ y $11$ son todos rojos y, en particular, el triángulo equilátero de vértices $3,6,11$ tiene todos sus vértices rojos.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 602
Sean $a,b,c,d$ cuatro números reales positivos. Si se cumple que
\[a+b+\frac{1}{ab}=c+d+\frac{1}{cd}\quad\text{y}\quad \frac{1}{a}+\frac{1}{b}+ab=\frac{1}{c}+\frac{1}{d}+cd,\]
demuestra que al menos dos de los cuatro números son iguales.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 603
Sea $ABC$ un triángulo con $AB\lt AC$ y sea $\Gamma$ su circunferencia circunscrita. Sean $D$, $E$ y $F$ los puntos de tangencia de la circunferencia inscrita de $ABC$ con $BC$, $CA$ y $AB$, respectivamente. Sea $R$ el punto de $EF$ tal que $DR$ es una altura del triángulo $DEF$ y sea $S$ el punto de corte de la bisectriz exterior del ángulo $BAC$ con $\Gamma$. Probar que $AR$ y $SD$ se cortan sobre $\Gamma$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Sesión 2 — 2 de abril de 2022
Problema 604
Sea $P$ un punto en el plano. Demuestra que es posible trazar tres semirrectas con origen en $P$ con la siguiente propiedad: para toda circunferencia de radio $r$ que contiene a $P$ en su interior, si $P_1$, $P_2$ y $P_3$ son los puntos de corte de las semirrectas con la circunferencia, entonces
\[|PP_1|+|PP_2|+|PP_3|\leq 3r.\]
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 605
En un grupo de 2022 estudiantes, algunos son amigos entre sí y la amistad es
siempre recíproca. Sabemos que cualquier subconjunto de esos estudiantes tiene
la siguiente propiedad: siempre existe un estudiante del subconjunto que es amigo
de, a lo sumo, $100$ estudiantes del mismo.
- Determina el menor entero positivo $N$ que nos asegura que se cumple la siguiente propiedad: es posible dividir a los estudiantes en $N$ grupos (no necesariamente del mismo tamaño), de manera que dos estudiantes que están en el mismo grupo nunca son amigos entre sí.
- Numeramos a los estudiantes del $1$ al $2022$. Sea $c_i$ el número de amigos del estudiante $i$. Determina el máximo valor que puede tomar la suma $c_1+c_2+\ldots+c_{2022}$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 606
Halla todas las ternas de enteros positivos $(x,y,z)$, con $z\gt 1$, que satisfacen
simultáneamente las siguientes tres condiciones:
\[x\text{ divide a }y+1,\qquad y\text{ divide a }z−1,\qquad z\text{ divide a }x^2+1.\]
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre